a) $$100\sqrt 3 \,m$$
b) $$\frac{{100}}{{\sqrt 3 }}\,m$$
c) $$50\sqrt 3 \,m$$
d) $$\frac{{200}}{{\sqrt 3 }}\,m$$

Answer: a
Explanation: Let AB be the tower and a point P at a distance of 100 m from its foot, angle of elevation of the top of the tower is 60°

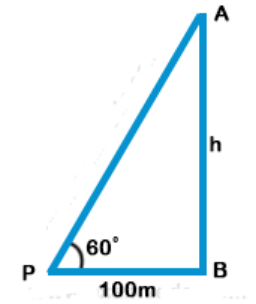
Let height of the tower = h
$$\eqalign{ & {\text{Then in right }}\Delta ABP \cr & \tan \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \frac{{AB}}{{PB}} \cr & \Rightarrow \tan {60^ \circ } = \frac{h}{{100}} \Rightarrow \sqrt 3 = \frac{h}{{100}} \cr & h = 100\sqrt 3 \cr & {\text{Height}}\,{\text{of}}\,{\text{tower}} = 100\sqrt 3 \cr} $$