a) $$\frac{a}{4}$$
b) $$\frac{a}{{\sqrt 2 }}$$
c) $$a\sqrt 2 $$
d) $$\frac{a}{{2\sqrt 2 }}$$

Answer: d
Explanation: Let AB and CD are two persons standing ‘a’ meters apart P is the mid-point of BD and from M, the angles of elevation of A and C are complementary

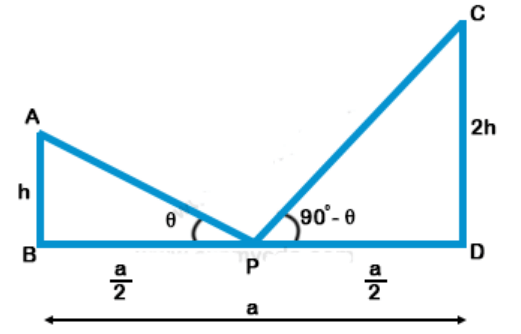
$$\eqalign{ & {\text{In}}\,\,\Delta {\text{APB,}} \cr & \tan \theta = \frac{{AB}}{{BP}} = \frac{h}{{\frac{a}{2}}} = \frac{{2h}}{a} \cr & {\text{In}}\,\,\Delta {\text{CDP,}} \cr & \cot (90 – \theta ) = \frac{{PD}}{{CD}} = \frac{{\frac{a}{2}}}{{2h}} = \frac{a}{{4h}} \cr & {\text{We}}\,\,{\text{Know}}\,\,{\text{that,}} \cr & \tan \theta = \cot (90 – \theta ). \cr & \frac{{2h}}{a} = \frac{a}{{4h}} \cr & 8{h^2} = {a^2} \cr & h = \frac{a}{{2\sqrt 2 }} \cr} $$