a) 141 m and 282 m
b) 70.5 m and 141 m
c) 65 m and 130 m
d) 130 m and 260 m

Answer: b
Explanation:

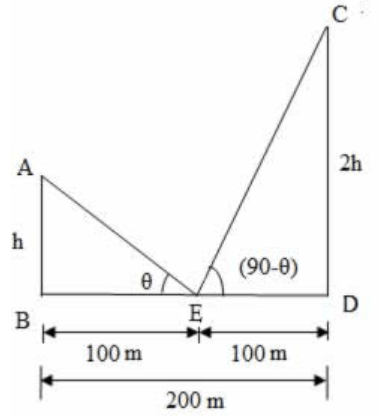
Let AB and CD be the poles with heights h and 2h respectively.
Given that distance between the poles, BD = 200 m
Let E be the middle point of BD,
∠ AEB = $$\theta $$
∠ CED = (90 – $$\theta $$)   ( given that angular elevations are complementary)
Since E is the middle point of BD, we have BE = ED = 100 m
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABE, \cr & \tan \theta = \frac{{AB}}{{BE}} \cr & \tan \theta = \frac{h}{{100}} \cr & h = 100\tan \theta \,……\left( 1 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta EDC, \cr & \tan\left( {90 – \theta } \right) = \frac{{CD}}{{ED}} \cr} $$
$$\cot \theta = \frac{{2h}}{{100}}$$     $$\left[ {\because \tan \left( {90 – \theta } \right) = \cot \theta } \right]$$
$$\eqalign{ & 2h = 100\cot \theta \,……\left( 2 \right) \cr & \left( 1 \right) \times \left( 2 \right) \cr} $$
$$ \Rightarrow 2{h^2} = {100^2}$$     $$\left[ {\because \tan \theta \times \cot\theta = \tan\theta \times \frac{1}{{\tan \theta }} = 1} \right]$$
$$\eqalign{ & \Rightarrow \sqrt 2 \,h = 100 \cr & \Rightarrow h = \frac{{100}}{{\sqrt 2 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{100 \times \sqrt 2 }}{{\sqrt 2 \times \sqrt 2 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 50\sqrt 2 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 50 \times 1.41 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 70.5 \cr & \Rightarrow 2h = 2 \times 70.5 = 141 \cr} $$
i.e. the height of the poles are 70.5 m and 141 m.