a) 9 m
b) 10.40 m
c) 15.57 m
d) 12 m

Answer: a
Explanation:

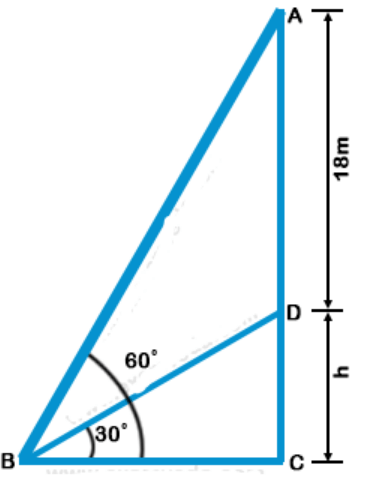
Let DC be the vertical tower and AD be the vertical flagpole. Let B be the point of observation.
Given that AD = 18 m, ∠ ABC = 60°, ∠ DBC = 30°
Let DC be h
$$\eqalign{ & \tan {30^ \circ } = \frac{{DC}}{{BC}} \cr & \frac{1}{{\sqrt 3 }} = \frac{h}{{BC}} \cr & h = \frac{{BC}}{{\sqrt 3 }}\,……\left( eq : 1 \right) \cr & \tan {60^ \circ } = \frac{{AC}}{{BC}} \cr & \sqrt 3 = \frac{{18 + h}}{{BC}} \cr & 18 + h = BC \times \sqrt 3 \,……\left( eq: 2 \right) \cr & \frac{eq : 1}{eq : 2} \Rightarrow \frac{h}{{18 + h}} = \frac{{\left( {\frac{{BC}}{{\sqrt 3 }}} \right)}}{{\left( {BC \times \sqrt 3 } \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{3} \cr & 3h = 18 + h \cr & 2h = 18 \cr & h = 9\,{\text{m}} \cr} $$
i.e., the height of the tower = 9 m