a) $$\frac{h}{2}\,m$$
b) $$\sqrt 3 \,h\,m$$
c) $$\frac{h}{3}\,m$$
d) $$\frac{h}{{\sqrt 3 }}\,m$$

Answer: c
Explanation: Let CD is the tower and A is a point such that the angle of elevation of C is 30°
B is and their point h m high of A and angle of depression of D is 60°

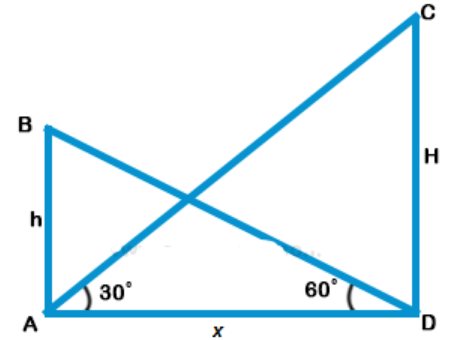
$$\eqalign{ & {\text{The}}\,AB = h\,m \cr & {\text{Let}}\,CD = H\,m\,\,\,{\text{and }}\,AD\, = x \cr & {\text{Now}}\,{\text{in}}\,{\text{right}}\,\Delta ABD, \cr & \tan \theta = \frac{{AB}}{{AD}} \cr & \tan {60^ \circ } = \frac{h}{x} \cr & \sqrt 3 = \frac{h}{x} \cr & \Rightarrow x = \frac{h}{{\sqrt 3 }}\,…….({\text{i}}) \cr & {\text{Similarly in right }}\Delta ACB, \cr & \tan {30^ \circ } = \frac{{CD}}{{AD}} \cr & \frac{1}{{\sqrt 3 }} = \frac{H}{x} \cr & x = \sqrt 3 \,H\,…….\left( {{\text{ii}}} \right) \cr & {\text{From}}\,\left( {\text{i}} \right)\,{\text{and}}\,\left( {{\text{ii}}} \right) \cr & \sqrt 3 \,H = \frac{h}{{\sqrt 3 }} \cr & H = \frac{h}{{\sqrt 3 \times \sqrt 3 }} = \frac{h}{3} \cr & {\text{Height of tower}} = \frac{h}{3} \cr} $$