1. A tank with capacity T liters is empty. If water flows into the tank from pipe X at the rate of x liters per minute and water is pumped out by Y at the rate of y liters per minute and x > y, then how many minutes will the tank be filled?
a) (x - y) 60 T minutes
b) (T - x) minutes
c) $$\frac{{\text{T}}}{{{\text{x}} - {\text{y}}}}$$ minutes
d) $$\frac{{\text{T}}}{{{\text{y}} - {\text{x}}}}$$ minutes
Discussion
Explanation: Net volume filled in 1 minute
= (x - y) liters
The tank will be filled in
= $$\frac{{\text{T}}}{{\left( {x - y} \right)}}$$ minutes
2. A pipe can fill a tank in 3 hours. There are two outlet pipes from the tank which can empty it in 7 and 10 hours respectively. If all the three pipes are opened simultaneously, then the tank will be filled in -
a) 8 hours
b) 9 hourss
c) 10 hours
d) 11 hours
Discussion
Explanation: Net part filled in 1 hour
$$\eqalign{ & {\text{ = }}\frac{1}{3} - \left( {\frac{1}{7} + \frac{1}{{10}}} \right) \cr & = \frac{1}{3} - \frac{{17}}{{70}} \cr & = \frac{{19}}{{210}} \cr} $$
The tank will be filled in $$\frac{{210}}{{19}}$$ hours i.e.
$$\eqalign{ & {\text{= 11}}\frac{1}{{19}}{\text{ hours}} \cr & \cong 11\,{\text{hours }} \cr} $$
3. A vessel has three pipes connected to it , two to supply liquid and one to draw liquid. The first alone can fill the vessel in $$4\frac{1}{2}$$ hours, the second in 3 hours and the third can empty it in $$1\frac{1}{2}$$ hours. If all the pipes are opened simultaneously when the vessel is half full, how soon will it be emptied?
a) $$4\frac{1}{2}$$ hours
b) $$5\frac{1}{2}$$ hours
c) $$6\frac{1}{2}$$ hours
d) None of these
Discussion
Explanation:
$$\eqalign{ & {\text{Net part filled in 1 hour}} \cr & = \frac{2}{3} - \left( {\frac{2}{9} + \frac{1}{3}} \right) \cr & = \left( {\frac{2}{3} - \frac{5}{9}} \right) \cr & = \frac{1}{9} \cr & \therefore \,\frac{1}{9}\,:\,\frac{1}{2}\,::\,1\,:\,x \cr & {\text{or}}\,\,\,x = \left( {\frac{1}{2} \times 9} \right) = 4\frac{1}{2}{\text{ hours}} \cr & {\text{So, the tank will be emptied in}} \cr & {\text{ = }}4\frac{1}{2}{\text{ hours}} \cr} $$
4. Two pipe A and B can fill a water tank in 20 and 24 minutes respectively and a third pipe C can empty at the rate of 3 gallons per minute. If A, B and C are open together to fill the tank in 15 minutes, find the capacity of tank?
a) 180 gallons
b) 150 gallons
c) 120 gallons
d) 60 gallons
Discussion
Explanation: Work done by the C pipe in 1 minute
$$\eqalign{ & = \frac{1}{{15}} - \left( {\frac{1}{{20}} + \frac{1}{{24}}} \right) \cr & = \left( {\frac{1}{{15}} - \frac{{11}}{{120}}} \right) \cr & = - \frac{1}{{40}}\,\left[ { - {\text{ve}}\,{\text{means}}\,{\text{emptying}}} \right] \cr} $$
Volume of $$\frac{1}{{40}}$$ part = 3 gallons.
Volume of whole = (3 × 40) gallons = 120 gallons
5. Three pipes P, Q and R can separately fill a cistern in 4, 8 and 12 hours respectively. Another pipe S can empty the completely filled cistern in 10 hours. Which of the following arrangements will fill the empty cistern in less time than others?
a) Q alone is open
b) P, R and S are open
c) P and S are open
d) P, Q and S are open
Discussion
Explanation:
$$\eqalign{ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(Total Capacity)}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{120}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\overline { \downarrow \,\,\,\,\,\,\,\,\,\, \downarrow \,\,\,\,\,\,\,\,\,\,\, \downarrow \,\,\,\,\,\,\,\,\,\,\,\,\, \downarrow } \cr & {\text{efficiency 30}}\,\,\,\,\,\,15\,\,\,\,\,\,\,\,10\,\,\, - 12 \cr & {\text{hours}} \to \,\,\mathop 4\limits_{\left( {\text{P}} \right)}^ \downarrow \,\,\,\,\,\,\mathop 8\limits_{\left( {\text{Q}} \right)}^ \downarrow \,\,\,\,\,\,\,\mathop {12}\limits_{\left( {\text{R}} \right)}^ \downarrow \,\,\,\,\,\,\,\,\,\,\,\mathop {10}\limits_{\left( {\text{S}} \right)}^ \downarrow \cr} $$
In order to fill the cistern in less time.
So, efficiency of filling should be more
now, check all options
(A) → Q efficiency 15 units/hr
(B) → (P + R - S) efficiency
= 30 + 10 - 12 = 28 units/hr
(C) → (P - S) efficiency
= 30 - 12 = 18 units/hr
(D) → (P + Q - S) efficiency
= 30 + 15 - 12 = 33 units/hr
Since efficiency of option (D) is highest.
6. Two pipes A and B can fill a tank in 20 and 30 hours respectively. Both the pipes are opened to fill the tank but when the tank is one - third full, a leak develops in the tank through which one - third water supplied by both the pipes gose out. The total time taken to fill the tank is?
a) 12 hours
b) 14 hours
c) 16 hours
d) 18 hours
Discussion
Explanation: Part filled by (A + B) in 1 hour
$$\eqalign{ & {\text{= }}\left( {\frac{1}{{20}} + \frac{1}{{30}}} \right) \cr & = \frac{1}{{12}} \cr} $$
So, A and B together can fill the tank in 12 hrs,
$$\frac{1}{3}$$ part is filled by (A + B) in
$$\left( {\frac{1}{3} \times 12} \right){\text{ = 4 hrs}}$$
Since the leak empties one - third water, so time taken to fill the tank
= Time taken by (A + B) to fill the whole tank + Time taken by (A + B) to fill one - third tank
= (12 + 4)
= 16 hours
7. Two pipes can fill a tank in 40 and 48 minutes respectively and a waste pipe can empty 3 gallons per minutes. All the three pipes working together can fill the tank in 30 minutes, The capacity of the tank is-
a) 60 gallons
b) 120 gallons
c) 180 gallons
d) 240 gallons
Discussion
Explanation: Work done by the waste pipe in 1 minute
$$\eqalign{ & {\text{ = }}\frac{1}{{30}} - \left( {\frac{1}{{40}} + \frac{1}{{48}}} \right) \cr & = \left( {\frac{1}{{30}} - \frac{{11}}{{220}}} \right) \cr & = - \frac{1}{{80}}\left[ { - \,{\text{Nagetive sign means emptying}}} \right] \cr & {\text{Volume of }}\frac{1}{{80}}{\text{ part = 3 galons}} \cr & {\text{Volume of whole tank}} \cr & {\text{ = }}\left( {3 \times 80} \right){\text{gallons}} \cr & {\text{ = 240 gallons}}{\text{}} \cr} $$
8. An outlet pipe can empty a cistern in 3 hours. In what time will empty $$\frac{2}{3}$$ of the cistern?
a) 3 hours
b) 5 hours
c) 2 hours
d) 4 hours
Discussion
Explanation: The outlet pipe empties the one complete cistern in 3 hours
Time taken to empty $$\frac{2}{3}$$ Part of the cistern
$$\eqalign{ & {\text{= }}\frac{2}{3} \times 3 \cr & = 2\,{\text{hours}} \cr} $$
9. A tank is 7 metre long and 4 meter wide wide. At what speed should water run through a pipe 5 cm broad and 4 cm deep so that in 6 hours and 18 minutes water level in the tank rises by 4.5 meter ?
a) 10 km/hours
b) 12 km/hours
c) 8 km/hours
d) None of these
Discussion
Explanation: Rate of flow of water = x cm/minute
Volume of water that flowed in the in 1 minutes
= (5 × 4 × x) = 20 x cu.cm.
Volume of water that flowed in the tank in 6 hours 18 minutes.
i.e. (6 × 60 + 18) = 378 minutes
= 2x × 378 cu. cm.
According to question,
$$\eqalign{ & {\text{20}}x \times 378 = 700 \times 400 \times 450 \cr & x = \left( {\frac{{700 \times 400 \times 450}}{{20 \times 378}}} \right){\text{cm /minutes}} \cr & x = \left( {\frac{{700 \times 400 \times 450 \times 60}}{{100000 \times 20 \times 378}}} \right){\text{km/hours}} \cr & x{\text{ = 10 km/hours}} \cr} $$
10. Two pipes can fill a tank in 12 hours and 16 hours respectively. A third pipe can empty the tank in 30 hours. If all three pipes are opened and functions simultaneously, how much time will the tank take to be full?( in hours )
a) $$10\frac{4}{9}$$
b) $$9\frac{1}{2}$$
c) $$8\frac{8}{9}$$
d) $$7\frac{2}{9}$$
Discussion
Explanation: First pipe fill the tank in 1 hour = $$\frac{1}{{12}}$$ part of tank
Second pipe fill the tank in 1 hour = $$\frac{1}{{16}}$$ part of tank
Third pipe empty the tank in 1 hour = $$\frac{1}{{30}}$$ part of tank
When all three pipes are opened simultaneously, part of the tank filled in 1 hour
$$ = \frac{1}{{12}} + \frac{1}{{16}} - \frac{1}{{30}}$$
LCM of 12, 16 and 30 = 240
$$\eqalign{ & {\text{ = }}\frac{{20 + 15 - 8}}{{240}} \cr & = \frac{{27}}{{240}} \cr} $$
Required time taken by all the three pipes
$${\text{ = }}\frac{{240}}{{27}} = \frac{{80}}{9} = 8\frac{8}{9}\,{\text{Hours}}$$
11. Two pipes can fill a tank in 20 and 24 minutes respectively and a waste pipe can empty 3 gallons per minute. All the three pipes working together can fill the tank in 15 minutes. The capacity of the tank is:
a) 60 gallons
b) 100 gallons
c) 120 gallons
d) 180 gallons
Discussion
Explanation: Work done by the waste pipe in 1 minute
$$\eqalign{ & = \frac{1}{{15}} - \left( {\frac{1}{{20}} + \frac{1}{{24}}} \right) \cr & = {\frac{1}{{15}} - \frac{{11}}{{120}}} \cr & = - \frac{1}{{40}}\,\,\,\,\,\left[ { - ve\,{\text{sign}}\,{\text{means}}\,{\text{emptying}}} \right] \cr & {\text{Volume}}\,{\text{of}}\,\frac{1}{{40}}{\text{part}} = 3\,{\text{gallons}} \cr & {\text{Volume}}\,{\text{of}}\,{\text{whole}} \cr & = \left( {3 \times 40} \right){\text{gallons}} \cr & = 120\,{\text{gallons}} \cr} $$
12. A tank is filled in 5 hours by three pipes A, B and C. The pipe C is twice as fast as B and B is twice as fast as A. How much time will pipe A alone take to fill the tank?
a) 20 hours
b) 25 hours
c) 35 hours
d) Cannot be determined
Discussion
Explanation: Suppose pipe A alone takes x hours to fill the tank.
Then, pipes B and C will take $$\frac{x}{2}$$ and $$\frac{x}{4}$$ hours respectively to fill the tank.
$$\eqalign{ & \frac{1}{x} + \frac{2}{x} + \frac{4}{x} = \frac{1}{5} \cr & \frac{7}{x} = \frac{1}{5} \cr & x = 35\,{\text{hours}} \cr} $$
13. Two pipes A and B together can fill a cistern in 4 hours. Had they been opened separately, then B would have taken 6 hours more than A to fill the cistern. How much time will be taken by A to fill the cistern separately?
a) 1 hours
b) 2 hours
c) 6 hours
d) 8 hours
Discussion
Explanation: Let the cistern be filled by pipe A alone in x hours.
Then, pipe B will fill it in (x + 6) hours
$$\eqalign{ & \frac{1}{x} + \frac{1}{{ {x + 6} }} = \frac{1}{4} \cr & \frac{{x + 6 + x}}{{x\left( {x + 6} \right)}} = \frac{1}{4} \cr & {x^2} - 2x - 24 = 0 \cr & \left( {x - 6} \right)\left( {x + 4} \right) = 0 \cr & x = 6\,{\kern 1pt} {\kern 1pt} \left[ {{\text{neglecting the negative value of }}x} \right] \cr} $$
14. Two pipes A and B can fill a tank in 20 and 30 minutes respectively. If both the pipes are used together, then how long will it take to fill the tank?
a) 12 minutes
b) 15 minutes
c) 25 minutes
d) 50 minutes
Discussion
Explanation: Part filled by A in 1 minute = $$\frac{1}{{20}}$$
Part filled by B in 1 minute = $$\frac{1}{{30}}$$
Part filled by (A + B) in 1 minute
$$\eqalign{ & = {\frac{1}{{20}} + \frac{1}{{30}}} = \frac{1}{{12}} \cr} $$
Both pipes can fill the tank in 12 minutes
15.Two pipes A and B can fill a tank in 15 minutes and 20 minutes respectively. Both the pipes are opened together but after 4 minutes, pipe A is turned off. What is the total time required to fill the tank?
a) 10 min. 20 sec.
b) 11 min. 45 sec.
c) 12 min. 30 sec
d) 14 min. 40 sec.
Discussion
Explanation:
$$\eqalign{ & {\text{Part}}\,{\text{filled}}\,{\text{in}}\,{\text{4}}\,{\text{minutes}} \cr & = 4\left( {\frac{1}{{15}} + \frac{1}{{20}}} \right) = \frac{7}{{15}} \cr & {\text{Remaining}}\,{\text{part}} = {1 - \frac{7}{{15}}} = \frac{8}{{15}} \cr & {\text{Part}}\,{\text{filled}}\,{\text{by}}\,B\,{\text{in}}\,{\text{1}}\,{\text{minute}} = \frac{1}{{20}} \cr & \frac{1}{{20}}:\frac{8}{{15}}::1:x \cr & x = {\frac{8}{{15}} \times 1 \times 20} \cr & \,\,\,\,\,\, = 10\frac{2}{3}\,\min \cr & \,\,\,\,\,\, = 10\min .\,40\,\sec . \cr & {\text{The}}\,{\text{tank}}\,{\text{will}}\,{\text{be}}\,{\text{full}}\,{\text{in}}\, = {4\min . + 10\min . +\, 40\sec .} \cr & = 14\min .\,40\sec . \cr} $$
16. A tank has a leak which would empty the completely filled tank in 10 hours. If the tank is full of water and a tap is opened which admits 4 litres of water per minute in the tank , the leak takes 15 hours to empty the tank. How many litres of water does the tank hold?
a) 2400 litters
b) 4500 litters
c) 1200 litters
d) 7200 litters
Discussion
Explanation: Let the total capacity of the tank is 30 units.
The efficiency of Leakage(Pipe A) will be $$\frac{30}{10}$$ = 3
And the efficiency of the leakage (Pipe A) and another Pipe (B) which is filling the tank will be $$\frac{30}{15}$$ = 2
Pipe A is emptying at 3 units/hr and when filling pipe B started then the emptying rate will come down to 2 units/hr.
Filling Pipe B efficiency is 3 - 2 = 1unit/hr
Pipe B will be fill the tank in $$\frac{30}{1}$$ = 30 hrs
Filling rate of Pipe B per minute is 4 litter
Total Capacity of tank will be = (4 × 60) × 30 = 7200 litters
17. A pump can fill a tank with water in 2 hours. Because of a leak, it took $$2\frac{1}{3}$$ hours to to fill the tank. The leak can drain all the water of the tank in?
a) $$4\frac{1}{3}$$ hours
b) 7 hour
c) 8 hour
d) 14 hour
Discussion
Explanation: Work done by the leak in 1 hour
$$\eqalign{ & {\text{ = }}\left( {\frac{1}{2} - \frac{3}{7}} \right) = \frac{1}{{14}} \cr} $$
Leak will empty the tank in 14 hours.
18. One pipe can fill a tank three times as fast as another pipe. If together the two pipes can fill the tank in 36 minutes, then the slower pipe alone will be able to fill the tank in-
a) 81 min
b) 108 min
c) 144 min
d) 192 min
Discussion
Explanation: Let the slower pipe alone fill the tank in x minutes
Then, Faster pipe alone will fill it in $$\frac{x}{3}$$ minutes
$$\eqalign{ & \frac{1}{x} + \frac{3}{x} = \frac{1}{{36}} \cr & \frac{4}{x} = \frac{1}{{36}} \cr & x = 144 \cr} $$
So slower pipe alone will fill the tank in 144 min.
19. A swimming pool is filled by three pipes with uniform flow. The first two pipes operating simultaneously fill the pool in the same time during which the pool is filled by the third pipe alone. The second pipe fills the pool 5 hours faster than the first pipe and 4 hours slower than the third pipe. The time required by the first pipe is?
a) 6 hours
b) 10 hours
c) 15 hours
d) 30 hours
Discussion
Explanation: Suppose first pipe alone takes x hours to fill the tank.
Then second and third pipes will takes (x - 5) and (x - 9) hours respectively to fill the tank.
$$\eqalign{ & \frac{1}{x} + \frac{1}{{\left( {x - 5} \right)}} = \frac{1}{{\left( {x - 9} \right)}} \cr & \frac{{x - 5 + x}}{{x\left( {x - 5} \right)}} = \frac{1}{{\left( {x - 9} \right)}} \cr & \left( {2x - 5} \right)\left( {x - 9} \right) = x\left( {x - 5} \right) \cr & {x^2} - 18x + 45 = 0 \cr & \left( {x - 15} \right)\left( {x - 3} \right) = 0 \cr & x = 15\left[ {{\text{neglecting }}x\,{\text{ = 3}}} \right] \cr} $$
So, first pipe alone takes 15 hrs to fill the tank.
20. 12 buckets of water fill a tank when the capacity of each bucket is 13.5 litres. How many buckets will be needed to fill the same tank, if the capacity of each bucket is 9 litres?
a) 8
b) 15
c) 16
d) 18
Discussion
Explanation: Capacity of the tank
= (12 × 13.5) litres
= 162 litres
Capacity of each bucket = 9 litres
Number of buckets needed
$$\eqalign{ & {\text{= }}\left( {\frac{{162}}{9}} \right) \cr & = 18 \cr} $$
21. Three pipes A, B and C can fill a tank from empty to full in 30 minutes, 20 minutes, and 10 minutes respectively. When the tank is empty, all the three pipes are opened. A, B and C discharge chemical solutions P, Q and R respectively. What is the proportion of the solution R in the liquid in the tank after 3 minutes?
a) $$\frac{5}{{11}}$$
b) $$\frac{6}{{11}}$$
c) $$\frac{7}{{11}}$$
d) $$\frac{8}{{11}}$$
Discussion
Explanation: Part filled by (A + B + C) in 3 minutes
$$\eqalign{ & = 3\left( {\frac{1}{{30}} + \frac{1}{{20}} + \frac{1}{{10}}} \right) \cr & = {3 \times \frac{{11}}{{60}}} = \frac{{11}}{{20}} \cr & {\text{Part}}\,{\text{filled}}\,{\text{by}}\,{\text{C}}\,{\text{in}}\,{\text{3}}\,{\text{minutes}} = \frac{3}{{10}} \cr & {\text{Required}}\,{\text{ratio}} \cr & = {\frac{3}{{10}} \times \frac{{20}}{{11}}} = \frac{6}{{11}} \cr} $$
22. Pipes A and B can fill a tank in 5 and 6 hours respectively. Pipe C can empty it in 12 hours. If all the three pipes are opened together, then the tank will be filled in:
a) $$1\frac{{13}}{{17}}$$ hours
b) $$2\frac{8}{{11}}$$ hours
c) $$3\frac{9}{{17}}$$ hours
d) $$4\frac{1}{2}$$ hours
Discussion
Explanation:
$$\eqalign{ & {\text{Net}}\,{\text{part}}\,{\text{filled}}\,{\text{in}}\,{\text{1}}\,{\text{hour}} \cr & = {\frac{1}{5} + \frac{1}{6} - \frac{1}{{12}}} = \frac{{17}}{{60}} \cr & {\text{The}}\,{\text{tank}}\,{\text{will}}\,{\text{be}}\,{\text{full}}\,{\text{in}}\,\frac{{60}}{{17}}\,{\text{hours}} \cr & i.e.,\,3\frac{9}{{17}}\,{\text{hours}} \cr} $$
Difference between their ages
$$\eqalign{ & = \left( {8x - 7x} \right) \cr & = {\text{ }}x\,{\text{years}} \cr & {\text{ = 2}}\,{\text{years}} \cr} $$
23. A pump can fill a tank with water in 2 hours. Because of a leak, it took $$2\frac{1}{3}$$ hours to fill the tank. The leak can drain all the water of the tank in:
a) $$4\frac{1}{3}$$ hours
b) 7 hours
c) 8 hours
d) 14 hours
Discussion
Explanation: Work done by the leak in 1 hour
$$\eqalign{ & = {\frac{1}{2} - \frac{3}{7}} = \frac{1}{{14}} \cr} $$
Leak will empty the tank in 14 hours
24. Two pipes A and B can fill a cistern in $$37\frac{1}{2}$$ minutes and 45 minutes respectively. Both pipes are opened. The cistern will be filled in just half an hour, if the B is turned off after:
a) 5 min.
b) 9 min.
c) 10 min.
d) 15 min.
Discussion
Explanation: Let B be turned off after x minutes.
Then, Part filled by (A + B) in x min. + Part filled by A in (30 - x) min. = 1
$$\eqalign{ & x\left( {\frac{2}{{75}} + \frac{1}{{45}}} \right) + \left( {30 - x} \right).\frac{2}{{75}} = 1 \cr & \frac{{11x}}{{225}} + \frac{{ {60 - 2x} }}{{75}} = 1 \cr & 11x + 180 - 6x = 225 \cr & x = 9 \cr} $$
25. A tank is filled by three pipes with uniform flow. The first two pipes operating simultaneously fill the tank in the same time during which the tank is filled by the third pipe alone. The second pipe fills the tank 5 hours faster than the first pipe and 4 hours slower than the third pipe. The time required by the first pipe is:
a) 6 hours
b) 10 hours
c) 15 hours
d) 30 hours
Discussion
Explanation: Suppose, first pipe alone takes x hours to fill the tank.
Then, Second and third pipes will take (x - 5) and (x - 9) hours respectively to fill the tank.
$$\eqalign{ & \frac{1}{x} + \frac{1}{{ {x - 5} }} = \frac{1}{{ {x - 9} }} \cr & \frac{{x - 5 + x}}{{x\left( {x - 5} \right)}} = \frac{1}{{ {x - 9} }} \cr & \left( {2x - 5} \right)\left( {x - 9} \right) = x\left( {x - 5} \right) \cr & {x^2} - 18x + 45 = 0 \cr & \left( {x - 15} \right)\left( {x - 3} \right) = 0 \cr & x = 15{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {{\text{neglecting}}\,x = 3} \right] \cr} $$
26. A tap can completely fill a water tank in 8 hours. The water tank has a hole in it through which the water leaks out. The leakage will cause the full water tank to get empty in 12 hours. How much time will it take for the tap the the tank completely with the hole?
a) 16 hours
b) 18 hours
c) 24 hours
d) None of these
Discussion
Explanation: Net part filled in 1 hour
$$\eqalign{ & {\text{ = }}\left( {\frac{1}{8} - \frac{1}{{12}}} \right) = \frac{1}{{24}} \cr} $$
The tank will be filled in 24 hours
27. A tank can be filled by pipe A in 2 hours and pipe B in 6 hours. At 10 A.M. pipe A was opened. At what time will the tank be filled if pipe B is opened at 11 A.M. ?
a) 12.45 A.M.
b) 5 P.M.
c) 11.45 A.M.
d) 12 P.M.
Discussion
Explanation:
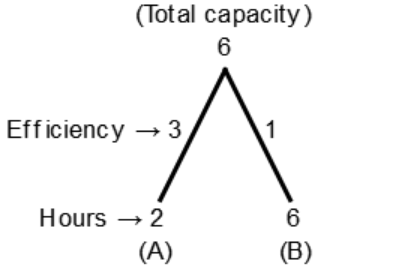
Pipe A will fill 3 units till 11 A.M. Remaining capacity
= 6 - 3
= 3 units
Now both pipes will fill the tank in
$$\frac{{{\text{Total Capacity}}}}{{{\text{Efficiency }}}} = \frac{3}{{\left( {3 + 1} \right)}} = \frac{3}{4}{\text{ hours}}$$
So, $$\left( {11 + \frac{3}{4}} \right)$$ A.M., tank will be filled = 11.45 A.M.
28. A water tank can be filled by a tap in 30 minutes and another tap can fill it in 60 minutes. If both taps are kept open for 5 minutes and then the first tap is closed, how long will it take foe the tank to be filled ?
a) 20 minutes
b) 25 minutes
c) 30 minutes
d) 45 minutes
Discussion
Explanation:
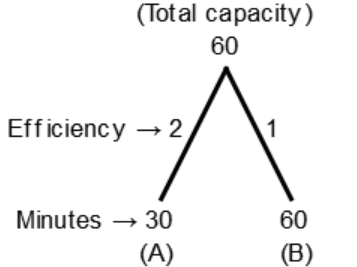
(A + B)'s filling (2 + 1) = 3 units/min
In 5 minutes they will fill 3 × 5 = 15 units
Remaining capacity = 60 - 15 = 45 units
Second pipe (B) fills it in
$$\eqalign{ & = \frac{{{\text{Remaining capacity}}}}{{{\text{efficiency of B}}}} \cr & = \frac{{45}}{1} \cr & = \,45\,{\text{minutes}} \cr} $$
29. A pipe can fill a tank in x hours and another can empty it in y hours. In how many hours they together fill it in ( y > x) ?
a) (x - y) hours
b) (y - x) hours
c) $$\left( {\frac{{xy}}{{x - y}}} \right)\,{\text{hours}}$$
d) $$\left( {\frac{{xy}}{{y - x}}} \right){\text{hours}}$$
Discussion
Explanation:
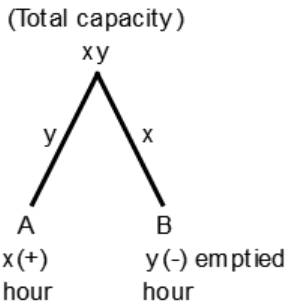
Time will be taken by both of them to fill the tank
$${\text{ = }}\frac{{xy}}{{y - x}}$$
30. A water tap fills a tub in 'p' hours and a sink at the bottom empties it in 'q' hours. If p < q and both tap and sink are opened the tank is filled in 'r' hours, then the relation between p, q, r :
a) $$\frac{1}{r} = \frac{1}{p} + \frac{1}{q}$$
b) $$\frac{1}{r} = \frac{1}{p} - \frac{1}{q}$$
c) $$r{\text{ = }}p{\text{ }} + {\text{ }}q$$
d) $${\text{ }}r{\text{ }} = {\text{ }}p{\text{ }} - {\text{ }}q$$
Discussion
Explanation:
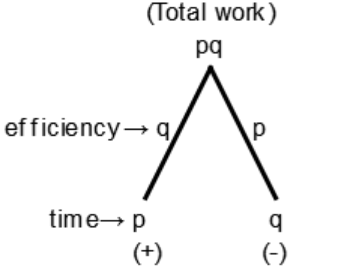
Net efficiency = q - p (∵ q > p)
Time required
$$\eqalign{ & {\text{r}} = \frac{{pq}}{{q - p}} \cr & or\,\frac{1}{r} = \frac{1}{p} - \frac{1}{q} \cr} $$
31.One pipe can fill a tank three times as fast as another pipe. If together the two pipes can fill the tank in 36 minutes, then the slower pipe alone will be able to fill the tank in:
a) 81 minutes
b) 108 minutes
c) 144 minutes
d) 192 minutes
Discussion
Explanation:
$$\eqalign{ & \frac{1}{x} + \frac{3}{x} = \frac{1}{{36}} \cr & \frac{4}{x} = \frac{1}{{36}} \cr & x = 144\,\text{minutes} \cr} $$
32. A large tanker can be filled by two pipes A and B in 60 minutes and 40 minutes respectively. How many minutes will it take to fill the tanker from empty state if B is used for half the time and A and B fill it together for the other half?
a) 15 minutes
b) 20 minutes
c) 27.5 minutes
d) 30 minutes
Discussion
Explanation:
$$\eqalign{ & {\text{Part}}\,{\text{filled}}\,{\text{by}}\,(A + B)\,{\text{in}}\,{\text{1}}\,{\text{minute}} \cr & = {\frac{1}{{60}} + \frac{1}{{40}}} = \frac{1}{{24}} \cr & {\text{Suppose}}\,{\text{the}}\,{\text{tank}}\,{\text{is}}\,{\text{filled}}\,{\text{in}}\,x\,{\text{minutes}} \cr & {\text{Then}},\,\frac{x}{2}\left( {\frac{1}{{24}} + \frac{1}{{40}}} \right) = 1 \cr & \frac{x}{2} \times \frac{1}{{15}} = 1 \cr & x = 30\,\text{minutes} \cr} $$
33. A tap can fill a tank in 6 hours. After half the tank is filled, three more similar taps are opened. What is the total time taken to fill the tank completely?
a) 3 hrs 15 min
b) 3 hrs 45 min
c) 4 hrs
d) 4 hrs 15 min
Discussion
Explanation: Time taken by one tap to fill half of the the tank = 3 hours
Part filled by the four taps in 1 hour
$$\eqalign{ & = {4 \times \frac{1}{6}} = \frac{2}{3} \cr & {\text{Remaining}}\,{\text{part}} = {1 - \frac{1}{2}} = \frac{1}{2} \cr & \frac{2}{3}:\frac{1}{2}::1:x \cr & \Rightarrow x = {\frac{1}{2} \times 1 \times \frac{3}{2}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{3}{4}\,hrs.\,\,i.e.,\,45\,\operatorname{mins} . \cr & {\text{So,}}\,{\text{total}}\,{\text{time}}\,{\text{taken}} = 3\,hrs.\,45\,mins. \cr} $$
34.Three taps A, B and C can fill a tank in 12, 15 and 20 hours respectively. If A is open all the time and B and C are open for one hour each alternately, the tank will be full in:
a) 6 hours
b) $$6\frac{2}{3}$$ hours
c) 7 hours
d) $$7\frac{1}{2}$$ hours
Discussion
Explanation:
$$\eqalign{ & \left( {{\text{A + B}}} \right){\text{'s 1 hour work}} \cr & {\text{ = }} {\frac{1}{{12}} + \frac{1}{{15}}} = \frac{9}{{60}} = \frac{3}{{20}} \cr & \left( {{\text{A + C}}} \right){\text{'s 1 hour work}} \cr & {\text{ = }} {\frac{1}{{12}} + \frac{1}{{20}}} = \frac{8}{{60}} = \frac{2}{{15}} \cr & {\text{Part filled in 2 hrs}} \cr & {\text{ = }} {\frac{3}{{20}} + \frac{2}{{15}}} = \frac{{17}}{{60}} \cr & {\text{Part filled in 6 hrs}} \cr & {\text{ = }} {3 \times \frac{{17}}{{60}}} = \frac{{17}}{{20}} \cr & {\text{Remaining part}} \cr & {\text{ = }} {1 - \frac{{17}}{{20}}} = \frac{3}{{20}} \cr} $$
Now it is the turn of A and B and
$$\frac{3}{{20}}$$ part is filled by A and B in 1 hour
Total time taken to fill tank
= (6 + 1) hrs
= 7 hrs
35. Three pipes A, B and C can fill a tank in 6 hours. After working at it together for 2 hours, C is closed and A and B can fill the remaining part in 7 hours. The number of hours taken by C alone to fill the tank is:
a) 10
b) 12
c) 14
d) 16
Discussion
Explanation: Part filled in 2 hours = $$\frac{2}{6}$$ = $$\frac{1}{3}$$
Remaining part = $$ {1 - \frac{1}{3}} $$ = $$\frac{2}{3}$$
(A + B)'s 7 hour's work = $$\frac{2}{3}$$
(A + B)'s 1 hour's work = $$\frac{2}{{21}}$$
C's 1 hour's work = {(A + B + C)'s 1 hour's work} - {(A + B's 1 hour's work}
$$\eqalign{ & = {\frac{1}{6} - \frac{2}{{21}}} \cr & = \frac{1}{{14}} \cr} $$
C alone can fill the tank in 14 hours
36. Three taps A, B, C can fill an overhead tank in 4, 6 and 12 hours respectively. How long would the three taps take to fill the tank if all of them are opened together ?
a) 2 hours
b) 4 hours
c) 3 hours
d) 5 hours
Discussion
Explanation:
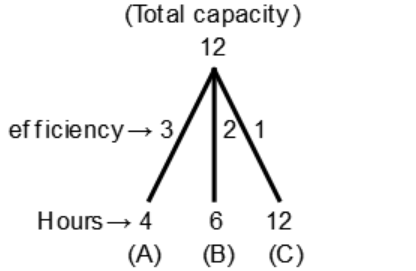
(A + B + C)'s efficiency
= 3 + 2 + 1
= 6 units/hr
(A + B + C) can fill the tank in
$$\eqalign{ & {\text{ = }}\frac{{{\text{Total Capacity}}}}{{{\text{Efficiency of}}\left( {{\text{A + B + C}}} \right){\text{ }}}} \cr & = \frac{{12}}{6} \cr & = 2{\text{ hours}} \cr} $$
37. Having the same capacity 9 taps fill up a water tank in 20 minutes. How many taps of the same capacity are required to fill up the same water tank in 15 minutes ?
a) 10 taps
b) 12 taps
c) 15 taps
d) 18 taps
Discussion
Explanation:
$$\eqalign{ & \left[ {\frac{{{m_1} \times {h_1} \times {t_1}}}{{{w_1}}} = \frac{{{m_2} \times {h_2} \times {t_2}}}{{{w_2}}}} \right] \cr & {9_{taps}} \times {20_{\min }} = {t_{taps}} \times {15_{\min }} \cr & t = 12\,\,{\text{taps}} \cr} $$
38. Pipe A can fill a tank in 4 hours and pipe B can fill it 6 hours. If they are opened on alternate hours and if pipe A is opened first then in how many hours, the tank shall be full ?
a) $${\text{4}}\frac{1}{2}$$ hours
b) $${\text{4}}\frac{2}{3}$$ hours
c) $${\text{3}}\frac{1}{2}$$ hours
d) $${\text{3}}\frac{1}{4}$$ hours
Discussion
Explanation: A → 4 hours
B → 6 hours
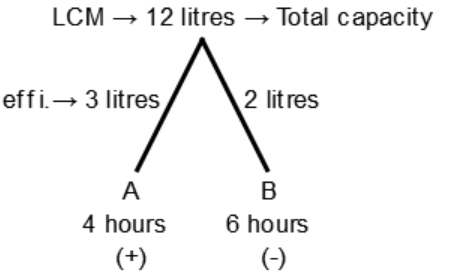
⇒ For the first hour tap A is opened and B for second hour
⇒ Work done by both in 2 hours
$$\eqalign{ & \to \left( {3\,{\text{lit/h}} + 2\,{\text{lit/h}}} \right) \times 2 = 10\,{\text{units}} \cr & \,\,\,\,\,\,\,\,\mathop {\,\,|\,\,\, \times 2}\limits_{{\text{4 hours}}}^{{\text{2 hours}}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathop {\,\,|\,\,\, \times 2}\limits_{{\text{10 litres}}}^{{\text{5 liters}}\,} \cr} $$
⇒ Remaining part
= 12 - 10 = 2 liters
⇒ Again 5th hour A will be opened Tap A will fill the 2 liters water with its efficiency = $$\frac{2}{3}$$ hours
Therefore tank will be filled in
= $$\left( {4 + \frac{2}{3}} \right)$$ hours
= $${\text{4}}\frac{2}{3}$$ hours
39. Pipe A can fill the tank in 8 hours and pipe B can fill it in 12 hours. If pipe A is opened at 7:00 AM and pipe B is opened at 9:00 AM, then at what time will the tank be full ?
a) 12:00 PM
b) 12:30 PM
c) 11:48 PM
d) 12:36 PM
Discussion
Explanation:
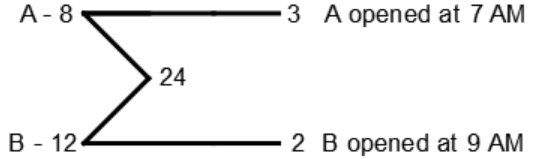
A opened 2 hours early to B
In 2 hours A can do 3 × 2 = 6 unit work
Remaining work = 24 - 6 = 18
A + B can do it in
$$\eqalign{ & = \frac{{18}}{5}{\text{hours}} \cr & = 3\frac{3}{5}{\text{hours}} \cr & {\text{ = 3}}\,{\text{hours 36 minutes}} \cr} $$
Tank will be full in 9 AM + 3 hours 36 minutes = 12.36 PM.
40. Two pipes A and B can fill a tank with water in 30 minutes and 45 minutes respectively. The third pipe C can empty the tank in 36 minutes. First A and B are opened. After 12 minutes C is opened. Total time ( in minutes ) in which the tank will be filled up is -
a) 12 minutes
b) 24 minutes
c) 30 minutes
d) 36 minutes
Discussion
Explanation:
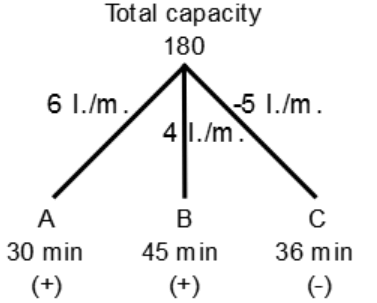
A . . . . . (+) 30 minutes
B . . . . . (+) 45 minutes
C . . . . . (-) 36 minutes
⇒ Water filled by (A + B) in 12 min
= 12 × (6 + 4)
= 12 × 10 = 120 liters
⇒ Remaining capacity
= 180 - 120 = 60 liters
⇒ After 12 minutes emptied pipe C is also opened
⇒ Total capacity (A + B - C)
= (6 + 4 - 5) = 5 liters/minutes
⇒ Time taken by (A + B - C) with capacity 5 liters/minutes to fill the remaining part
$$ = \frac{{60\,\,{\text{liters}}}}{{5\,\,{\text{liters/minutes}}}}{\text{ = 12 minutes}}$$
⇒ Therefore, total time in which the tank will be filled up is
= 12 + 12
= 24 minutes