PrepBharat

1. Tree top’s angle of elevation is 30° from a point on ground, 300m away the tree. When the tree grew up its angle of elevation became 60° from the same point. How much did the tree grow?
a) $$100\sqrt 3 \,{\text{m}}$$
b) $${\text{200}}\sqrt 3 \,{\text{m}}$$
c) $$300\frac{1}{{\sqrt 3 }}\,{\text{m}}$$
d) $$\frac{{200}}{{\sqrt 3 }}\,{\text{m}}$$

View Answer  Discussion

Answer: b
Explanation:

$$\eqalign{ & {\text{Original tree height}} = {\text{h}} = {\text{MQ}} \cr & {\text{New}}\,{\text{tree}}\,{\text{height}} = PQ \cr & {\text{in}}\,\Delta MQN,\,\tan {30^ \circ } = \frac{1}{{\sqrt 3 }} = \frac{{MQ}}{{NQ}} \cr & MQ = \frac{{300}}{{\sqrt 3 }} \cr & {\text{in}}\,\Delta PQN,\,\tan {60^ \circ } = \sqrt 3 = \frac{{PQ}}{{NQ}} \cr & PQ = 300\sqrt 3 \cr & {\text{Tree}}\,{\text{grew}} = PQ - MQ \cr & {\text{Tree}}\,{\text{grew}} = 300\sqrt 3 - \frac{{300}}{{\sqrt 3 }} \cr & = 300\frac{2}{{\sqrt 3 }} \cr & = 3 \times 100 \times \frac{2}{{\sqrt 3 }} \cr & = 200\sqrt 3 \,{\text{m}} \cr} $$

2. TheMohan looks at a tree top and the angle made is 45°. He moves 10 cm back and again looks at the tree top but this time angle made is 30°. How high is the tree top from ground?
a) $$\frac{{10}}{{\sqrt 3 + 1}}\,{\text{cm}}$$
b) $$20\sqrt 3 \,{\text{cm}}$$
c) $$20\,{\text{cm}}$$
d) $$\frac{{10}}{{\sqrt 3 - 1}}\,{\text{cm}}$$

View Answer  Discussion

Answer: d
Explanation:

Let PQ be three and M and N be positions where Mphan stands.
$$\eqalign{ & {\text{Now,}}\,{\text{tan}}{45^ \circ } = 1 = \frac{{PQ}}{{MQ}} \cr & PQ = MQ \cr & \tan {30^ \circ } = \frac{1}{{\sqrt 3 }} = \frac{{PQ}}{{NQ}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{PQ}}{{10 + MQ}} \cr & 10 + MQ = \sqrt 3 \,PQ \cr} $$
$$ 10 + PQ = \sqrt 3 \,PQ$$     (As, PQ = MQ)
$$ PQ = \frac{{10}}{{\sqrt 3 - 1}}\,{\text{cm}}$$

3. Rohit while seeing a bird on tree top made 45° angle of elevation. He walks 240ft. towards the tree to observe the bird closely, thus making 60° angle of elevation. How far was Rohit from the tree initially?
a) $$\frac{{240\sqrt 3 }}{{\sqrt 3 - 1}}\,{\text{ft}}$$
b) $$\frac{{240}}{{\sqrt 3 - 1}}\,{\text{ft}}$$
c) $$\frac{{240}}{{\sqrt 3 }}\,{\text{ft}}$$
d) $$240\sqrt 3 \,{\text{ft}}$$

View Answer  Discussion

Answer: a
Explanation:

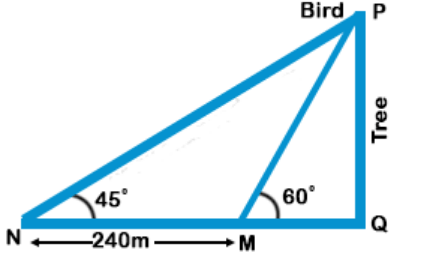
$$\eqalign{ & {\text{Now,}}\,{\text{tan}}{45^ \circ } = 1 = \frac{{PQ}}{{NQ}} \cr & {\text{Tree}}\,{\text{height}} \cr & = PQ = NQ \cr & = \left( {240 + MQ} \right) \cr & \tan {60^ \circ } = \sqrt 3 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{PQ}}{{MQ}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{240 + MQ}}{{MQ}} \cr & 240 + MQ = \sqrt 3 \,MQ \cr & MQ = \frac{{240}}{{\sqrt 3 - 1}}\,{\text{ft}} \cr & NQ = 240 + MQ \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{240\sqrt 3 }}{{\sqrt 3 - 1}}\,{\text{ft}} \cr} $$
= Rohit was this much far away initially

4. A tree breaks and falls to the ground such that its upper part is still partially attached to its stem. At what height did it break, if the original height of the tree was 24 cm and it makes an angle of 30° with the ground?
a) 12 cm
b) 8 cm
c) 9.5 cm
d) 7.5 cm

View Answer  Discussion

5. Two houses are in front of each other. Both have chimneys on their top. The line joining the chimneys makes an angle of 45° with the ground. How far are the houses from each other if one house is 25m and other is 10m in height?
a) 18 m
b) 12 m
c) 7.5 m
d) 15 m

View Answer  Discussion

Answer: d
Explanation:

In ∠ABR, ∠ARB = 90° and ∠BAR = 45°
Sum of angles of a triangle = 180°
So ∠ABR = 180 - 90 - 45 = 45°
BR = AR
AS = RQ = 10m
Also, BR = BQ - RQ = 25 - 10 = 15m
AR = 15m = Distance between houses

6. Shadow of a man is $$\frac{1}{{\sqrt 3 }}$$ times the height of the man. What will be the sun’s angle of elevation?
a) 135°
b) 45°
c) 30°
d) 60°

View Answer  Discussion

7. There is a tree between houses of A and B. If the tree leans on A’s House, the tree top rests on his window which is 12 m from ground. If the tree leans on B’s House, the tree top rests on his window which is 9 m from ground. If the height of the tree is 15 m, what is distance between A’s and B’s house?
a) 21 m
b) 25 m
c) 16 m
d) 12 m

View Answer  Discussion

Answer: a
Explanation:

In $$\Delta $$STR, by Pythagoras theorem
$$\eqalign{ & R{T^2} = S{T^2} + R{S^2} \cr & S{T^2} = {15^2} - {9^2} = 144 \cr & ST = 12\,{\text{m}} \cr} $$
In $$\Delta $$TQP, by Pythagoras theorem
$$\eqalign{ & P{T^2} = T{Q^2} + P{Q^2} \cr & T{Q^2} = {15^2} - {12^2} = 81 \cr & TQ = 9\,{\text{m}} \cr} $$
Distance between houses
SQ = ST + TQ
SQ = 12 + 9
SQ = 21 m

8. Ramesh and Suresh’s mud forts have heights 8 cm and 15 cm. They are 24 cm apart. How far are the fort tops from each other?
a) 31 cm
b) 24cm
c) 25 cm
d) 24.5 cm

View Answer  Discussion

Answer: c
Explanation:

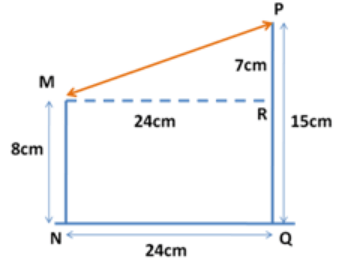
Let MN = Ramesh's fort & PQ = Suresh's fort
From the diagram we can see that
MR = 24 cm & PR = 15 - 8 = 7 cm
By Pythagoras theorem,
Hypotenuse² = (side1)² + (side2)²
$$\eqalign{ & {\text{MP}} = \sqrt {{{24}^2} + {7^2}} \cr & {\text{MP}} = 25\,{\text{cm}} \cr} $$

9. A and B are standing on ground 50 meters apart. The angles of elevation for these two to the top of a tree are 60° and 30°. What is height of the tree?
a) $$50\sqrt 3 \,{\text{m}}$$
b) $$\frac{{25}}{{\sqrt 3 }}\,{\text{m}}$$
c) $$25\sqrt 3 \,{\text{m}}$$
d) $$\frac{{25}}{{\sqrt 3 - 1}}\,{\text{m}}$$

View Answer  Discussion

10.There is a tower of 10m between two parallel roads. The angles of depression of the roads from the top of the tower are 30° and 45°. How far are the roads from each other?
a) 27.32 m
b) 29.56 m
c) $$20\sqrt 3 \,{\text{m}}$$
d) $$\frac{{10}}{{\sqrt 3 }}\,{\text{m}}$$

View Answer  Discussion

Answer: a
Explanation:

Angle of Depression = Angle of Elevation
Tower PS = 10 m in height
$$\eqalign{ & {\text{tan}}{45^ \circ } = 1 = \frac{{PS}}{{RS}} \cr & PS = RS = 10 \cr & \tan {30^ \circ } = \frac{1}{{\sqrt 3 }} = \frac{{PS}}{{SQ}} = \frac{{10}}{{SQ}} \cr & SQ = 10\sqrt 3 \cr & RQ = RS + SQ \cr & \,\,\,\,\,\,\,\,\,\,\, = 10 + 10\sqrt 3 \cr & \,\,\,\,\,\,\,\,\,\,\, = 27.32\,{\text{m}} \cr} $$

11.A flagstaff is placed on top of a building. The flagstaff and building subtend equal angles at a point on level ground which is 200 m away from the foot of the building. If the height of the flagstaff is 50 m and the height of the building is h, which of the following is true?
a) h³ - 50h² + (200)²h + (200)²50 = 0
b) h³ - 50h² - (200)²h + (200)²50 = 0
c) h³ + 50h² + (200)²h - (200)²50 = 0
d) None of these

View Answer  Discussion

Answer: c
Explanation:

Let AD be the flagstaff and CD be the building.
Assume that the flagstaff and building subtend equal angles at point B.
Given that AD = 50 m, CD = h and BC = 200 m
Let ∠ABD = $$\theta $$, ∠DBC = $$\theta $$   ( flagstaff and building subtend equal angles at a point on level ground).
Then, ∠ABC = 2$$\theta $$
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta BCD, \cr & \tan \theta = \frac{{DC}}{{BC}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{h}{{200}}\,......\left( 1 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta BCA, \cr & \tan 2\theta = \frac{{AC}}{{BC}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{AD + DC}}{{200}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{50 + h}}{{200}} \cr} $$
$$ \Rightarrow \frac{{2\tan \theta }}{{1 - {{\tan }^2}\theta }} = \frac{{50 + h}}{{200}}$$      $$\left( {\because \tan \left( {2\theta } \right) = \frac{{2\tan \theta }}{{1 - {{\tan }^2}\theta }}} \right)$$
$$\frac{{2\left( {\frac{h}{{200}}} \right)}}{{1 - \frac{{{h^2}}}{{{{200}^2}}}}} = \frac{{50 + h}}{{200}}$$      ( substituted value of tan $$\theta $$ from eq:1)
$$\eqalign{ & 2h = \left( {1 - \frac{{{h^2}}}{{{{200}^2}}}} \right)\,\left( {50 + h} \right) \cr & 2h = 50 + h - \frac{{50{h^2}}}{{{{200}^2}}} - \frac{{{h^3}}}{{{{200}^2}}} \cr} $$
$$ 2\left( {{{200}^2}} \right)h = 50{\left( {200} \right)^2} + $$     $$h{\left( {200} \right)^2} - $$   $$50{h^2} - {h^3}$$
( multiplied LHS and RHS by $${{{200}^2}}$$ )

h³ + 50h² + (200)²h - (200)²50 = 0

12. From the top of a hill 100 m high, the angles of depression of the top and bottom of a pole are 30° and 60° respectively. What is the height of the pole
a) 52 m
b) 50 m
c) 66.67 m
d) 33.33 m

View Answer  Discussion

Answer: c
Explanation:

Consider the diagram shown above. AC represents the hill and DE represents the pole
Given that AC = 100 m
∠XAD = ∠ADB = 30° ( AX || BD )
∠XAE = ∠AEC = 60° ( AX || CE)
Let DE = h
Then, BC = DE = h,
AB = (100 - h)   (∵ AC = 100 and BC = h),
BD = CE
$$\eqalign{ & \tan {60^ \circ } = \frac{{AC}}{{CE}} \cr & \sqrt 3 = \frac{{100}}{{CE}} \cr & CE = \frac{{100}}{{\sqrt 3 }}\,......\left( 1 \right) \cr & \tan {30^ \circ } = \frac{{AB}}{{BD}} \cr & \frac{1}{{\sqrt 3 }} = \frac{{100 - h}}{{BD}} \cr} $$
$$ \frac{1}{{\sqrt 3 }} = \frac{{100 - h}}{{\left( {\frac{{100}}{{\sqrt 3 }}} \right)}}$$      ( BD = CE and substituted the value of CE from eq. 1)
$$\eqalign{ & \Rightarrow \left( {100 - h} \right) = \frac{1}{{\sqrt 3 }} \times \frac{{100}}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{100}}{3} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 33.33 \cr & \Rightarrow h = 100 - 33.33 = 66.67\,{\text{m}} \cr} $$
i.e., the height of the pole = 66.67 m

13.A poster is on top of a building. Rajesh is standing on the ground at a distance of 50 m from the building. The angles of elevation to the top of the poster and bottom of the poster are 45° and 30° respectively. What is the height of the poster?
a) $$\frac{{50}}{{\sqrt 3 }}\left( {\sqrt 3 - 1} \right)$$
b) $$10\sqrt 3 \,{\text{m}}$$
c) $$50\sqrt 3 \,{\text{m}}$$
d) None of these

View Answer  Discussion

Answer: a
Explanation:

$$\eqalign{ & {\text{in}}\,\Delta PNQ,\,\tan {45^ \circ } = \frac{{PQ}}{{NQ}} \cr & PQ = NQ = 50{\text{m}} \cr & {\text{in}}\,\Delta MNQ,\,\tan {30^ \circ } = \frac{{MQ}}{{NQ}} \cr & \frac{1}{{\sqrt 3 }} = \frac{{MQ}}{{50}} \cr & MQ = \frac{{50}}{{\sqrt 3 }} \cr & h = PM \cr & \,\,\,\,\,\,\,\,\,\, = PQ - MQ \cr & \,\,\,\,\,\,\,\,\,\, = 50 - \frac{{50}}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\, = \frac{{50}}{{\sqrt 3 }}\left( {\sqrt 3 - 1} \right) \cr} $$
Poster height = $$\frac{{50}}{{\sqrt 3 }}\left( {\sqrt 3 - 1} \right)$$

14. Angles of elevation of pole are 60° and 45° from points at distances m and n on ground respectively. Here m, when measured from base of pole is less than n. What is the height of the pole?
a) $$\sqrt {mn\sqrt 3 } \,{\text{units}}$$
b) $$\sqrt {mn\root 4 \of 3 } \,{\text{units}}$$
c) $$\sqrt {3mn} \,{\text{units}}$$
d) $$\sqrt {mn} \,{\text{units}}$$

View Answer  Discussion

Answer: a
Explanation:

$$\eqalign{ & {\text{Height}}\,{\text{of}}\,{\text{pole}} = PQ \cr & \tan {60^ \circ } = \sqrt 3 = \frac{{PQ}}{m} \cr & \tan {45^ \circ } = 1 = \frac{{PQ}}{n} \cr & {\text{Multiply}}\,{\text{both}}\,{\text{equations}} \cr & \sqrt 3 \times 1 = \frac{{PQ}}{m} \times \frac{{PQ}}{n} \cr & PQ = \sqrt {mn\sqrt 3 } \,{\text{units}} \cr} $$

15. A tree is cut partially and made to fall on ground. The tree however does not fall completely and is still attached to its cut part. The tree top touches the ground at a point 10m from foot of the tree making an angle of 30°. What is the length of the tree?
a) $$10\sqrt 3 \,{\text{m}}$$
b) $$\frac{{10}}{{\sqrt 3 }}\,{\text{m}}$$
c) $$\frac{{\left( {\sqrt 2 - 1} \right)}}{{10}}\,{\text{m}}$$
d) $$\frac{{10}}{{\sqrt 2 }}\,{\text{m}}$$

View Answer  Discussion

16. The top of a 15 metre high tower makes an angle of elevation of 60° with the bottom of an electric pole and angle of elevation of 30° with the top of the pole. What is the height of electric pole ?
a) 5 meters
b) 8 meters
c) 10 meters
d) 12 meters

View Answer  Discussion

17. TF is a tower with F on the ground. The angle of elevation of T from A is x° such that tan x°= $$\frac{2}{5}$$   and AF = 200 m. The angle of elevation of T from a nearer point B is y° with BF = 80 m. The value of y° is-
a) 75°
b) 45°
c) 60°
d) 30°

View Answer  Discussion

18. From the top of a tower, the angles of depression of two objects P and Q (situated on the ground on the same side of the tower) separated at a distance of 100$${\left( {3 - \sqrt 3 } \right)}$$   m are 45° and 60 ° respectively. The height of the tower is-
a) 200 m
b) 250 m
c) 300 m
d) None of these

View Answer  Discussion

Answer: c
Explanation:

$$\eqalign{ & {\text{Let, }}OP = {\text{ }}a \cr & {\text{tan }}{60^ \circ } = \frac{H}{a} \cr & H = \sqrt 3 a \cr & \frac{H}{{\sqrt 3 }} = a.....(i) \cr} $$
$$tan{45^ \circ } = 1$$   $$ = \frac{H}{{a + 100\left( {3 - \sqrt 3 } \right)}}$$
$$ a + 100\left( {3 - \sqrt 3 } \right) = H$$
From (i) $$\frac{H}{{\sqrt 3 }} + $$   $$100\left( {3 - \sqrt 3 } \right)$$   = H
$$\eqalign{ & H + 300\sqrt 3 - 300 = \sqrt 3 H \cr & 300\sqrt 3 - 300 = \sqrt 3 H - H \cr & \left( {\sqrt 3 - 1} \right)H = 300\left( {\sqrt 3 - 1} \right) \cr & H = 300{\text{ m}} \cr} $$

19. From a lighthouse the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the lighthouse is h metres, the distance between the ships is
a) $$\left( {\sqrt 3 + 1} \right)\,h\,{\text{metres}}$$
b) $$\left( {\sqrt 3 - 1} \right)\,h\,{\text{metres}}$$
c) $$\sqrt 3 \,h\,{\text{metres}}$$
d) $${\text{1 + }}\left( {1 + \frac{1}{{\sqrt 3 }}} \right)\,h\,{\text{metres}}$$

View Answer  Discussion

Answer: a
Explanation: Let AB be lighthouse and P and Q are two ships on its opposite sides which form angle of elevation of A as 45° and 30° respectively AB = h
Let PB = x and QB = y


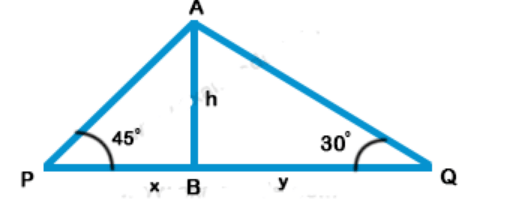
$$\eqalign{ & {\text{Now in right }}\Delta APB \cr & \tan \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \frac{{AB}}{{PB}} \cr & \Rightarrow \tan {45^ \circ } = \frac{h}{x} \Rightarrow 1 = \frac{h}{x} \cr & \Rightarrow x = h\,............(i) \cr & {\text{Similarly in right }}\Delta AQB, \cr & \tan {30^ \circ } = \frac{{AP}}{{QB}} = \frac{h}{y} \cr & \frac{1}{{\sqrt 3 }} = \frac{h}{y} \cr & y = \sqrt 3 \,h\,..............(ii) \cr & {\text{Adding (i) and (ii)}} \cr & PQ = x + y \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = h + \sqrt 3 \,h \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {\sqrt 3 + 1} \right)\,h \cr} $$

20. If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground, then the height of the lamp-post is
a) 1.5 m
b) 2 m
c) 2.5 m
d) 2.8 m

View Answer  Discussion

Answer: c
Explanation: Let AB is girls and CD is lamp-post AB = 1.5 which casts her shadow EB

$$\eqalign{ & EB = 4.5\,m,\,BD = 3\,m \cr & {\text{Now in }}\Delta AEB \cr & \tan \theta = \frac{{AB}}{{BE}} = \frac{{1.5}}{{4.5}} = \frac{1}{3} \cr & {\text{and in }}\Delta CED \cr & \tan \theta = \frac{{CD}}{{ED}} \Rightarrow \frac{1}{3} = \frac{h}{{4.5 + 3}} \cr & \Rightarrow \frac{1}{3} = \frac{h}{{7.5}} \cr & \Rightarrow h = \frac{{7.5}}{3} - 2.5\,m \cr & {\text{Height of lamp - post}} = {\text{2}}{\text{.5}}\,m \cr} $$

21.The ratio of the length of a rod and its shadow is 1 : $$\sqrt 3 $$ The angle of elevation of the sum is
a) 30°
b) 45°
c) 60°
d) 90°

View Answer  Discussion

Answer: a
Explanation: Let AB be rod and BC be its shadow
So that AB : BC = 1 : $$\sqrt 3 $$
Let $$\theta $$ be the angle of elevation

$$\eqalign{ & \tan \theta = \frac{{AB}}{{BC}} = \frac{1}{{\sqrt 3 }} = \tan {30^ \circ } \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {\because \tan {{30}^ \circ } = \frac{1}{{\sqrt 3 }}} \right) \cr & \theta = {30^ \circ } \cr} $$
Hence angle of elevation $$ = {30^ \circ }$$

22. It is found that on walking x metres towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60° . The height of the chimney is
a) $$3\sqrt 2 \,x$$
b) $$2\sqrt 3 \,x$$
c) $$\frac{{\sqrt 3 }}{2}\,x$$
d) $$\frac{2}{{\sqrt 3 }}\,x$$

View Answer  Discussion

Answer: c
Explanation: In the figure, AB is chimney and CB and DB are its shadow

$$\eqalign{ & \tan {60^ \circ } = \frac{{AB}}{{BC}} = \frac{h}{{BC}} \cr & \sqrt 3 = \frac{h}{{BC}} \cr & \Rightarrow BC = \frac{h}{{\sqrt 3 }}\,.......\,\left( {\text{i}} \right) \cr & {\text{and}} \cr & \tan {30^ \circ } = \frac{h}{{DB}} = \frac{h}{{DB + BC}} \cr & \frac{1}{{\sqrt 3 }} = \frac{h}{{x + BC}} \cr & x + BC = h\sqrt 3 \cr & \Rightarrow BC = h\sqrt 3 - x\,.......\,\left( {{\text{ii}}} \right) \cr & {\text{From}}\,\left( {\text{i}} \right)\,{\text{and}}\,\left( {{\text{ii}}} \right) \cr & \frac{h}{{\sqrt 3 }} = h\sqrt 3 - x \cr & \Rightarrow \frac{h}{{\sqrt 3 }} - h\sqrt 3 = - x \cr & x = h\sqrt 3 - \frac{h}{{\sqrt 3 }} \cr & x = h\left( {\sqrt 3 - \frac{1}{{\sqrt 3 }}} \right) \cr & x = h\frac{{3 - 1}}{{\sqrt 3 }} \cr & x = \frac{{2h}}{{\sqrt 3 }} \cr & h = \frac{{\sqrt 3 }}{2}x \cr} $$

23. A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
a) $$\frac{4}{{\sqrt 3 }}$$
b) $$4\sqrt 3 $$
c) $$2\sqrt 2 $$
d) $$4$$

View Answer  Discussion

24. The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
a) 12 m
b) 10 m
c) 8 m
d) 6 m

View Answer  Discussion

Answer: a
Explanation: Let AB and CD be two poles
AB = 20 m, CD = 14 m
A and C are joined by a wire
CE || DB and angle of elevation of A is 30°
Let CE = DB = x and AC = L

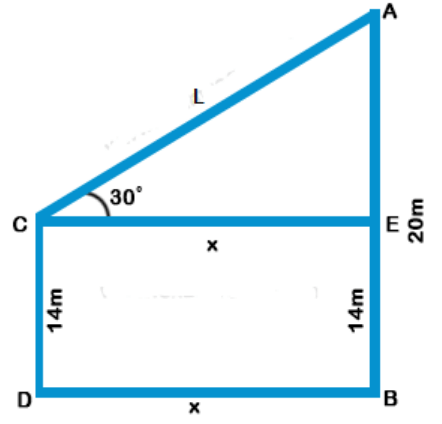
Now AE = AB - EB = AB - CD = 20 - 14 = 6 m
$$\eqalign{ & {\text{Now in right }}\Delta ACE, \cr & \sin \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}} = \frac{{AE}}{{AC}} \cr & \sin {30^ \circ } = \frac{6}{{AC}} \cr & \frac{1}{2} = \frac{6}{{AC}} \cr & \Rightarrow AC = 2 \times 6 = 12 \cr & {\text{Length of AC}} = 12\,m \cr} $$

25. A lower subtends an angle of 30° at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60°. The height of the tower is
a) $$\frac{h}{2}\,m$$
b) $$\sqrt 3 \,h\,m$$
c) $$\frac{h}{3}\,m$$
d) $$\frac{h}{{\sqrt 3 }}\,m$$

View Answer  Discussion

Answer: c
Explanation: Let CD is the tower and A is a point such that the angle of elevation of C is 30°
B is and their point h m high of A and angle of depression of D is 60°

$$\eqalign{ & {\text{The}}\,AB = h\,m \cr & {\text{Let}}\,CD = H\,m\,\,\,{\text{and }}\,AD\, = x \cr & {\text{Now}}\,{\text{in}}\,{\text{right}}\,\Delta ABD, \cr & \tan \theta = \frac{{AB}}{{AD}} \cr & \tan {60^ \circ } = \frac{h}{x} \cr & \sqrt 3 = \frac{h}{x} \cr & \Rightarrow x = \frac{h}{{\sqrt 3 }}\,.......({\text{i}}) \cr & {\text{Similarly in right }}\Delta ACB, \cr & \tan {30^ \circ } = \frac{{CD}}{{AD}} \cr & \frac{1}{{\sqrt 3 }} = \frac{H}{x} \cr & x = \sqrt 3 \,H\,.......\left( {{\text{ii}}} \right) \cr & {\text{From}}\,\left( {\text{i}} \right)\,{\text{and}}\,\left( {{\text{ii}}} \right) \cr & \sqrt 3 \,H = \frac{h}{{\sqrt 3 }} \cr & H = \frac{h}{{\sqrt 3 \times \sqrt 3 }} = \frac{h}{3} \cr & {\text{Height of tower}} = \frac{h}{3} \cr} $$

26. An observer 2 m tall is $$10\sqrt 3 $$  m away from a tower. The angle of elevation from his eye to the top of the tower is 30º. The height of the tower is:
a) 14 m
b) 12 m
c) 10 m
d) None of these

View Answer  Discussion

27. A person, standing exactly midway between two towers, observes the top of the two towers at angle of elevation of 22.5° and 67.5°. What is the ratio of the height of the taller tower to the height of the shorter tower? (Given that tan 22.5° = $$\sqrt 2 - 1$$ )
a) $$1 - 2\sqrt 2 :1$$
b) $$1 + 2\sqrt 2 :1$$
c) $$3 + 2\sqrt 2 :1$$
d) $$3 - 2\sqrt 2 :1$$

View Answer  Discussion

Answer: c
Explanation:

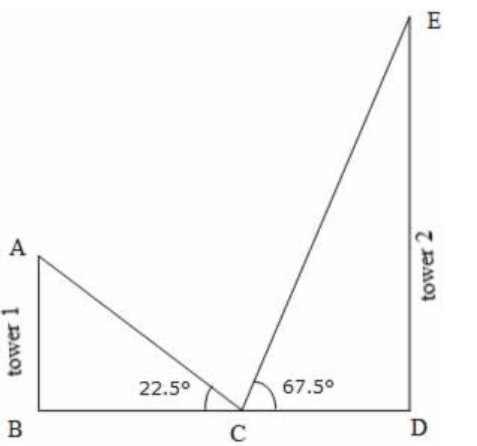
Let ED be the taller tower and AB be the shorter tower.
Let C be the point of observation
Given that ∠ ACB = 22.5° and ∠ DCE = 67.5°
Given that C is the midpoint of BD
Hence, BC = CD
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,ABC, \cr & \tan{22.5^ \circ } = \frac{{AB}}{{BC}}\,.....\left( {eq:1} \right)\, \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,CDE, \cr & \tan {67.5^ \circ } = \frac{{ED}}{{CD}}\,.....\left( {eq:2} \right) \cr & \frac{{\left( {eq:2} \right)}}{{\left( {eq:1} \right)}} \Rightarrow \frac{{\tan {{67.5}^ \circ }}}{{\tan{{22.5}^ \circ }}} = \frac{{\left( {\frac{{ED}}{{CD}}} \right)}}{{\left( {\frac{{AB}}{{BC}}\,} \right)}} \cr & = \frac{{ED}}{{AB}}\,\,\,\,\,\left( { CD = BC} \right) \cr & \Rightarrow \frac{{\tan \left( {{{90}^ \circ } - {{22.5}^ \circ }} \right)}}{{\tan {{22.5}^ \circ }}} = \frac{{ED}}{{AB}} \cr & \Rightarrow \frac{{\cot {{22.5}^ \circ }}}{{\tan {{22.5}^ \circ }}} = \frac{{ED}}{{AB}} \cr & \,\,\,\,\,\,\,\,\,\,\left[ {\because \tan \left( {90 - \theta } \right) = \cot \theta } \right] \cr & \Rightarrow \frac{{\left( {\frac{1}{{\tan {{22.5}^ \circ }}}} \right)}}{{\tan {{22.5}^ \circ }}} = \frac{{ED}}{{AB}} \cr & \,\,\,\,\,\,\,\,\,\,\,\left[ {\because \cot \theta = \frac{1}{{\tan \theta }}} \right] \cr & \Rightarrow \frac{{ED}}{{AB}} = \frac{1}{{{{\left( {\tan {{22.5}^ \circ }} \right)}^2}}} \cr & = \frac{1}{{{{\left( {\sqrt 2 - 1} \right)}^2}}} \cr & = {\left( {\frac{1}{{\sqrt 2 - 1}}} \right)^2} \cr & = {\left[ {\frac{{\left( {\sqrt 2 + 1} \right)}}{{\left( {\sqrt 2 - 1} \right)\left( {\sqrt 2 + 1} \right)}}} \right]^2} \cr & = {\left[ {\frac{{\left( {\sqrt 2 + 1} \right)}}{{\left( {2 - 1} \right)}}} \right]^2} \cr & = {\left[ {\frac{{\left( {\sqrt 2 + 1} \right)}}{1}} \right]^2} \cr & = {\left( {\sqrt 2 + 1} \right)^2} \cr & = \left( {2 + 2\sqrt 2 + 1} \right) \cr & = \left( {3 + 2\sqrt 2 } \right) \cr & {\text{Required}}\,{\text{Ratio}} \cr & = ED:AB \cr & = \left( {3 + 2\sqrt 2 } \right):1 \cr} $$

28. A vertical tower stands on ground and is surmounted by a vertical flagpole of height 18 m. At a point on the ground, the angle of elevation of the bottom and the top of the flagpole are 30° and 60° respectively. What is the height of the tower
a) 9 m
b) 10.40 m
c) 15.57 m
d) 12 m

View Answer  Discussion

Answer: a
Explanation:

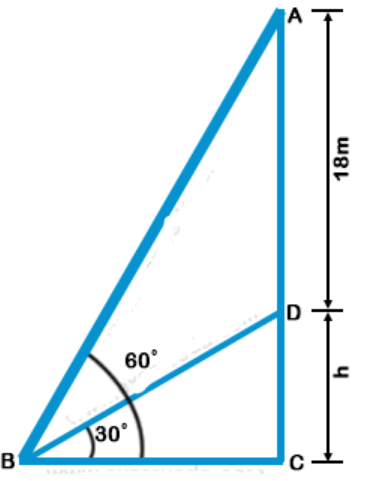
Let DC be the vertical tower and AD be the vertical flagpole. Let B be the point of observation.
Given that AD = 18 m, ∠ ABC = 60°, ∠ DBC = 30°
Let DC be h
$$\eqalign{ & \tan {30^ \circ } = \frac{{DC}}{{BC}} \cr & \frac{1}{{\sqrt 3 }} = \frac{h}{{BC}} \cr & h = \frac{{BC}}{{\sqrt 3 }}\,......\left( eq : 1 \right) \cr & \tan {60^ \circ } = \frac{{AC}}{{BC}} \cr & \sqrt 3 = \frac{{18 + h}}{{BC}} \cr & 18 + h = BC \times \sqrt 3 \,......\left( eq: 2 \right) \cr & \frac{eq : 1}{eq : 2} \Rightarrow \frac{h}{{18 + h}} = \frac{{\left( {\frac{{BC}}{{\sqrt 3 }}} \right)}}{{\left( {BC \times \sqrt 3 } \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{3} \cr & 3h = 18 + h \cr & 2h = 18 \cr & h = 9\,{\text{m}} \cr} $$
i.e., the height of the tower = 9 m

29. To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and he is 5 m away from the wall, what is the length of the window?
a) 8.65 m
b) 2 m
c) 2.5 m
d) 3.65 m

View Answer  Discussion

Answer: d
Explanation:

Let AB be the man and CD be the window
Given that the height of the man, AB = 180 cm, the distance between the man and the wall, BE = 5 m,
∠ DAF = 45°, ∠ CAF = 60°
From the diagram, AF = BE = 5 m
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,AFD, \cr & \tan {45^ \circ } = \frac{{DF}}{{AF}} \cr & 1 = \frac{{DF}}{5} \cr & DF = 5\,......\left( 1 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,AFC, \cr & \tan {60^ \circ } = \frac{{CF}}{{AF}} \cr & \sqrt 3 = \frac{{CF}}{5} \cr & CF = 5\sqrt 3 \,......\,\left( 2 \right) \cr & {\text{Length}}\,{\text{of}}\,{\text{the}}\,{\text{window}} \cr & = CD = \left( {CF - DF} \right) \cr} $$
  $$ = 5\sqrt 3 - 5$$     [ Substituted the value of CF and DF from (1) and (2)]
$$\eqalign{ & = 5\left( {\sqrt 3 - 1} \right) \cr & = 5\left( {1.73 - 1} \right) \cr & = 5 \times 0.73 \cr & = 3.65\,{\text{m}} \cr} $$

30. When the sun's altitude changes from 30° to 60°, the length of the shadow of a tower decreases by 70m. What is the height of the tower?
a) 35 m
b) 140 m
c) 60.6 m
d) 20.2 m

View Answer  Discussion

Answer: c
Explanation:


Let AD be the tower, BD be the initial shadow and CD be the final shadow.
Given that BC = 70 m, ∠ ABD = 30°, ∠ ACD = 60°,
Let CD = x, AD = h
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,CDA \cr & \tan {60^ \circ } = \frac{{AD}}{{CD}} \cr & \sqrt 3 = \frac{h}{x}\,......\left( {eq:1} \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,BDA \cr & \tan {30^ \circ } = \frac{{AD}}{{BD}} \cr & \frac{1}{{\sqrt 3 }} = \frac{h}{{70 + x}}\,......\left( {eq:2} \right) \cr & \frac{{eq:1}}{{eq:2}} \Rightarrow \frac{{\sqrt 3 }}{{\left( {\frac{1}{{\sqrt 3 }}} \right)}} = \frac{{\left( {\frac{h}{x}} \right)}}{{\left( {\frac{h}{{70 + x}}} \right)}} \cr & \Rightarrow 3 = \frac{{70 + x}}{x} \cr & \Rightarrow 2x = 70 \cr & \Rightarrow x = 35 \cr} $$
Substituting this value of x in eq : 1, we have
$$\eqalign{ & \sqrt 3 = \frac{h}{{35}} \cr & \Rightarrow h = 35\sqrt 3 = 35 \times 1.73 \cr & = 60.55 \approx 60.6 \cr} $$

31. Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is: ages is:
a) 173 m
b) 200 m
c) 273 m
d) 300 m

View Answer  Discussion

32. A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30º with the man's eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 60º. What is the distance between the base of the tower and the point P?
a) 4 √3 units
b) 8 units
c) 12 units
d) Data inadequate

View Answer  Discussion

Answer: d
Explanation: One of AB, AD and CD must have given.

So, the data is inadequate.

33. The angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:
a) 2.3 m
b) 4.6 m
c) 7.8 m
d) 9.2 m

View Answer  Discussion

Answer: d
Explanation: Let AB be the wall and BC be the ladder.

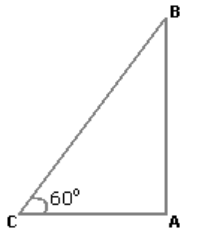
Then, ∠ACB = 60° = AC = 4.6m
$$\frac{{AC}}{{BC}} = \cos {60^ \circ } = \frac{1}{2}$$
⇒ BC = 2 × AC = 2 × 4.6 = 9.2m

34. An observer 1.6 m tall is 20√3 away from a tower. The angle of elevation from his eye to the top of the tower is 30º. The heights of the tower is:
a) 21.6 m
b) 23.2 m
c) 24.72 m
d) None of these

View Answer  Discussion

Answer: a
Explanation: Let AB be the observer and CD be the tower.

Draw BE ⊥ CD
Then CE = AB = 1.6m
BE = AC = 20√3m
$$\frac{{DE}}{{BE}} = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }}$$
$$ \Rightarrow DE = \frac{{BE}}{{\sqrt 3 }} = \frac{{20\sqrt 3 }}{{\sqrt 3 }} = 20$$
CD = CE + DE = (1.6 + 20) m = 21.6 m

35.From a point P on a level ground, the angle of elevation of the top tower is 30º. If the tower is 100 m high, the distance of point P from the foot of the tower is:
a) 149 m
b) 156 m
c) 173 m
d) 200 m

View Answer  Discussion

Answer: c
Explanation: Let AB be the tower

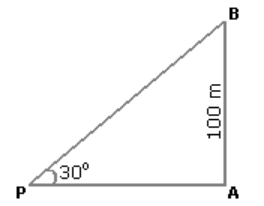
Then, ∠APB = 30° and AB = 100m
$$\frac{{AB}}{{AP}} = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }}$$
⇒ AP = AB × √3 = 100 × √3
AP = 100 × 1.73 = 173m

36. If the angles of elevation of a tower from two points distance a and b (a > b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is?
a) $$\sqrt {a + b} $$
b) $$\sqrt {ab} $$
c) $$\sqrt {a - b} $$
d) $$\sqrt {\frac{a}{b}} $$

View Answer  Discussion

Answer: b
Explanation: Let AB be the tower and P and Q are such points that PB = a, QB = b and angles of elevation at P and Q are 30° and 60° respectively

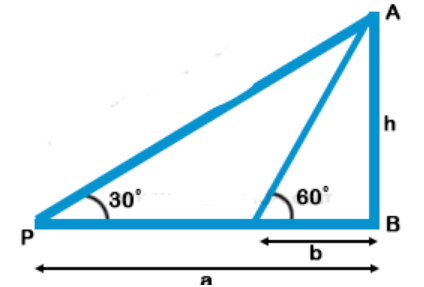
$$\eqalign{ & {\text{Let }}AB = h \cr & {\text{Now in right }}\Delta APB, \cr & \tan \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \frac{{AB}}{{PB}} \cr & \Rightarrow \tan {30^ \circ } = \frac{h}{a} \cr & \Rightarrow \frac{1}{{\sqrt 3 }} = \frac{h}{a}\,...........(i) \cr & {\text{Similarly in right }}\Delta AQB, \cr & \tan {60^ \circ } = \frac{{AB}}{{QB}} \cr & \Rightarrow \sqrt 3 = \frac{h}{b}\,...........(ii) \cr & {\text{Multiplying (i) and (ii)}} \cr & \frac{1}{{\sqrt 3 }} \times \sqrt 3 = \frac{h}{a} \times \frac{h}{b} \cr & 1 = \frac{{{h^2}}}{{ab}} \cr & {h^2} = ab \cr & h = \sqrt {ab} \cr & {\text{Height of the tower}} = \sqrt {ab} \cr} $$

37. A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
a) $$15\sqrt 3 \,m$$
b) $$\frac{{15\sqrt 3 }}{2}\,m$$
c) $$\frac{{15}}{2}\,m$$
d) $$15\,m$$

View Answer  Discussion

Answer: b
Explanation: Let AB is a wall and AC is the ladder 15 m long which makes an angle of 60° with the ground

In ∆ABC, ∠B = 90°
Let height of wall AB = h
Then
$$\sin \theta = \frac{{AB}}{{AC}} \Rightarrow \sin {60^ \circ } = \frac{h}{{15}}$$
$$\eqalign{ & \frac{{\sqrt 3 }}{2} = \frac{h}{{15}} \cr & h = \frac{{15\sqrt 3 }}{2}\,m \cr} $$
Height of the wall $$ = \frac{{15\sqrt 3 }}{2}\,m $$

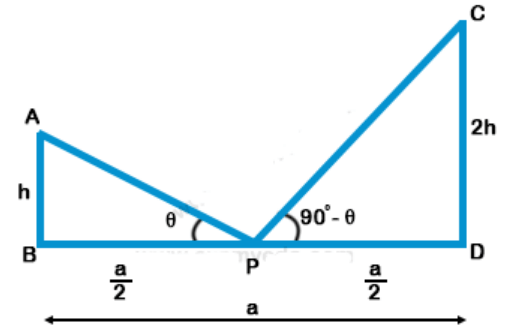
38. Two poles are ‘a’ metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
a) $$\sqrt {2a} \,{\text{metres}}$$
b) $$\frac{a}{{2\sqrt 2 }}\,{\text{metres}}$$
c) $$\frac{a}{{\sqrt 2 }}\,{\text{metres}}$$
d) $$2a\,{\text{metres}}$$

View Answer  Discussion

Answer: b
Explanation: Let height of pole CD = h
and AB = 2h, BD = a
M is mid-point of BD

$$ DM = MB = \frac{a}{2}$$
$${\text{Let }}\angle CMD = \theta ,$$    $${\text{then }}\angle AMB = $$     $${90^ \circ } - \theta $$
$$\eqalign{ & \tan \theta = \frac{{CD}}{{DM}} = \frac{h}{{\frac{a}{2}}} = \frac{{2h}}{a}\,......({\text{i}}) \cr & {\text{and}} \cr & tan\left( {{{90}^ \circ } - \theta } \right) = \frac{{AB}}{{MB}} = \frac{{2h}}{{\frac{a}{2}}} = \frac{{4h}}{a} \cr & \Rightarrow \cot \theta = \frac{{4h}}{a}\,..........({\text{ii}}) \cr & {\text{Multiplying (i) and (ii)}} \cr & {\text{tan}}\theta \times {\text{cot}}\theta = \frac{{2h}}{a} \times \frac{{4h}}{a} \cr & 1 = \frac{{8{h^2}}}{{{a^2}}} = {h^2} = \frac{{{a^2}}}{8}\,m \cr & h = \sqrt {\frac{{{a^2}}}{8}} = \frac{a}{{\sqrt 8 }} = \frac{a}{{2\sqrt 2 }}\,m \cr} $$

39. From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
a) 25 m
b) 50 m
c) 75 m
d) 100 m

View Answer  Discussion

Answer: b
Explanation: Let AB be the tower and CD be cliff Angle of elevation of A is equal to the angle of depression of B at C
Let angle be Q and CD = 25 m

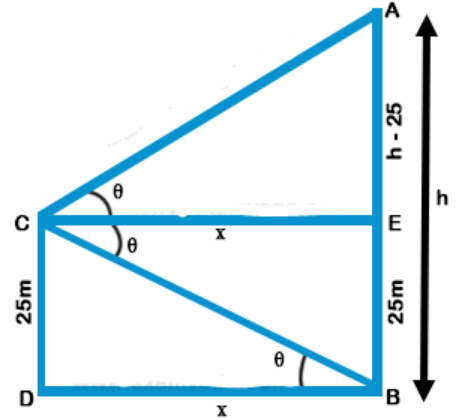
$$\eqalign{ & {\text{Let}}\,AB = h \cr & CE \,\, || \,\, DB \cr & EC = DB = x{\text{ }}\left( {{\text{suppose}}} \right) \cr & EB = CD = 25 \cr & AE = h - 25 \cr & {\text{Now in right }}\Delta CDB, \cr & \tan \theta = \frac{{CD}}{{DB}} = \frac{{25}}{x}\,......\left( {\text{i}} \right) \cr & {\text{and in right }}\Delta CAE \cr & \tan \theta = \frac{{AE}}{{CE}} = \frac{{h - 25}}{x}\,......\left( {{\text{ii}}} \right) \cr & {\text{From}}\left( {\text{i}} \right){\text{ and }}\left( {{\text{ii}}} \right) \cr & \frac{{25}}{x} = \frac{{h - 25}}{x} \cr & 25 = h - 25 \cr & h = 25 + 25 = 50 \cr & {\text{Height of tower}} = 50\,m \cr} $$

40. The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45°. Then the height of the tower (in metres) is
a) $$50\sqrt 3 $$
b) $$50$$
c) $$\frac{{50}}{{\sqrt 2 }}$$
d) $$\frac{{50}}{{\sqrt 3 }}$$

View Answer  Discussion

Answer: b
Explanation: Let AB be tower and C is a point on the ground 50 m away

From foot of tower B
Angle of elevation is 45°
Let h be height of tower = x m
$$\eqalign{ & \tan \theta = \frac{{AB}}{{BC}} \cr & \tan {45^ \circ } = \frac{{AB}}{50} \cr & 1 = \frac{{AB}}{{50}} \Rightarrow AB = 50\,m \cr} $$

41. A vertical pole fixed to the ground is divided in the ratio 1 : 9 by a mark on it with lower part shorter than the upper part. If the two parts subtend equal angles at a place on the ground, 15 m away from the base of the pole, what is the height of the pole ?
a) $$60\sqrt 5 \,{\text{m}}$$
b) $${\text{15}}\sqrt 5 \,{\text{m}}$$
c) $$15\sqrt 3 \,{\text{m}}$$
d) $${\text{60}}\sqrt 3 \,{\text{m}}$$

View Answer  Discussion

Answer: a
Explanation:

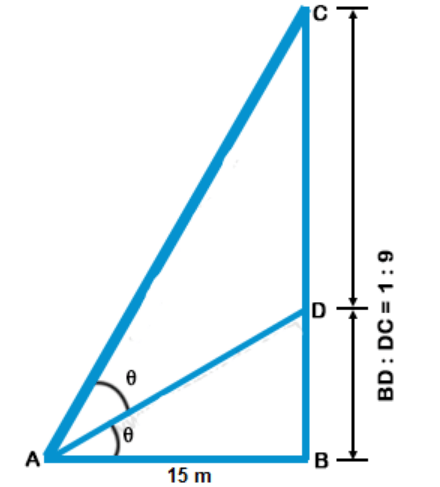
Let CB be the pole and point D divides it such that BD : DC = 1 : 9
Given that AB = 15 m
Let the the two parts subtend equal angles at point A such that ∠ CAD = ∠ BAD = $$\theta $$
From "Angle Bisector Theorem", we have
$$\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}$$
$$ \Rightarrow \frac{1}{9} = \frac{{15}}{{AC}}$$     [ BD : DC = 1 : 9 and AB = 15(given)]
$$ \Rightarrow AC = 15 \times 9\,{\text{m}}\,......\left( {eq:1} \right)$$
$${\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABC,$$
$$CB = \sqrt {A{C^2} - A{B^2}} $$     ( Pythagorean theorem)
$$ = \sqrt {{{\left( {15 \times 9} \right)}^2} - {{15}^2}} $$     [AC=15 × 9(eq : 1) and AB=15 m(given)]
$$\eqalign{ & = \sqrt {{{15}^2} \times {9^2} - {{15}^2}} \cr & = \sqrt {{{15}^2}\left( {{9^2} - 1} \right)} \cr & = \sqrt {{{15}^2} \times 80} \cr & = \sqrt {{{15}^2} \times 16 \times 5} \cr & = 15 \times 4 \times \sqrt 5 \cr & = 60\sqrt 5 \,{\text{m}} \cr} $$

42. A man is watching from the top of a tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man's eye when at a distance of 100 metres from the tower. After 10 seconds, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming that it is running in still water?
a) 26.28 km/hr
b) 32.42 km/hr
c) 24.22 km/hr
d) 31.25 km/hr

View Answer  Discussion

Answer: a
Explanation:

Consider the diagram shown above.
Let AB be the tower. Let C and D be the positions of the boat
Then, ∠ ACB = 45°, ∠ ADC = 30°, BC = 100 m
$$\eqalign{ & \tan {45^ \circ } = \frac{{AB}}{{BC}} \cr & 1 = \frac{{AB}}{{100}} \cr & AB = 100\,......\left( {eq:1} \right) \cr} $$
$$\tan {30^ \circ } = \frac{{AB}}{{BD}}$$
$$ \frac{1}{{\sqrt 3 }} = \frac{{100}}{{BD}}$$     ( Substituted the value of AB from equation 1)
$$ BD = 100\sqrt 3 $$
$$\eqalign{ & CD = \left( {BD - BC} \right) \cr & \,\,\,\,\,\,\,\,\,\,\, = \left( {100\sqrt 3 - 100} \right) \cr & \,\,\,\,\,\,\,\,\,\,\, = 100\left( {\sqrt 3 - 1} \right) \cr} $$
It is given that the distance CD is covered in 10 seconds.
i.e., the distance $$100\left( {\sqrt 3 - 1} \right)$$     is covered in 10 seconds.
$$\eqalign{ & {\text{Required}}\,{\text{speed}} = \frac{{{\text{Distance}}}}{{{\text{Time}}}} \cr & = \frac{{100\left( {\sqrt 3 - 1} \right)}}{{10}} \cr & = 10\left( {1.73 - 1} \right) \cr & = 7.3\,{\text{meter/seconds}} \cr & = 7.3 \times \frac{{18}}{5}\,{\text{km/hr}} \cr & = 26.28\,{\text{km/hr}} \cr} $$

43. An aeroplane when 900 m high passes vertically above another aeroplane at an instant when their angles of elevation at same observing point are 60° and 45° respectively. Approximately, how many meters higher is the one than the other?
a) 381 m
b) 169 m
c) 254 m
d) 211 m

View Answer  Discussion

Answer: a
Explanation:

Let C and D be the position of the aeroplanes.
Given that CB = 900 m, ∠ CAB = 60°, ∠ DAB = 45°
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABC, \cr & \tan {60^ \circ } = \frac{{CB}}{{AB}} \cr & \sqrt 3 = \frac{{900}}{{AB}} \cr & AB = \frac{{900}}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\, = \frac{{900 \times \sqrt 3 }}{{\sqrt 3 \times \sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\, = \frac{{900\sqrt 3 }}{3} \cr & \,\,\,\,\,\,\,\,\,\, = 300\sqrt 3 \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABD, \cr & \tan {45^ \circ } = \frac{{DB}}{{AB}} \cr & 1 = \frac{{DB}}{{AB}} \cr & DB = AB = 300\sqrt 3 \cr & {\text{Required}}\,{\text{height}} = CD \cr & = \left( {CB - DB} \right) \cr & = \left( {900 - 300\sqrt 3 } \right) \cr & = \left( {900 - 300 \times 1.73} \right) \cr & = \left( {900 - 519} \right) \cr & = 381\,{\text{m}} \cr} $$

44. The angle of elevation of the sun, when the length of the shadow of a tree is equal to the height of the tree, is:
a) 30°
b) 60°
c) 45°
d) None of these

View Answer  Discussion

Answer: c
Explanation:

Consider the diagram shown above where QR represents the tree and PQ represents its shadow
$$\eqalign{ & {\text{We}}\,{\text{have}},\,QR = PQ \cr & {\text{Let}}\,\angle QPR = \theta \cr} $$
$$\tan \theta = \frac{{QR}}{{PQ}} = 1$$     (since QR = PQ)
$$ \theta = {45^ \circ }$$
i.e., required angle of elevation = 45°

45. Two persons are on either sides of a tower of height 50 m. The persons observers the top of the tower at an angle of elevation of 30° and 60°. If a car crosses these two persons in 10 seconds, what is the speed of the car?
a) $$24\sqrt 3 \,{\text{km/hr}}$$
b) $$\frac{{20\sqrt 3 }}{3}\,{\text{km/hr}}$$
c) $$\frac{{24}}{{\sqrt 3 }}\,{\text{km/hr}}$$
d) None of these

View Answer  Discussion

Answer: a
Explanation:

Let BD be the tower and A and C be the positions of the persons.
Given that BD = 50 m, ∠ BAD = 30°, ∠ BCD = 60°
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,ABD, \cr & \tan {30^ \circ } = \frac{{BD}}{{BA}} \cr & \frac{1}{{\sqrt 3 }} = \frac{{50}}{{BA}} \cr & BA = 50\sqrt 3 \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta CBD, \cr & \tan {60^ \circ } = \frac{{BD}}{{BC}} \cr & \sqrt 3 = \frac{{50}}{{BC}} \cr & \Rightarrow BC = \frac{{50}}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{50 \times \sqrt 3 }}{{\sqrt 3 \times \sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{50\sqrt 3 }}{3} \cr} $$
Distance between the two persons
$$\eqalign{ & = AC = BA + BC \cr & = 50\sqrt 3 + \frac{{50\sqrt 3 }}{3} \cr & = \sqrt 3 \left( {50 + \frac{{50}}{3}} \right) \cr & = \frac{{200\sqrt 3 }}{3}\,{\text{m}} \cr} $$
i.e., the distance travelled by the car in 10 seconds = $$\frac{{200\sqrt 3 }}{3}\,{\text{m}}$$
$$\eqalign{ & {\text{Speed}}\,{\text{of the car}} = \frac{{{\text{Distance}}}}{{{\text{Time}}}} \cr & = \frac{{\left( {\frac{{200\sqrt 3 }}{3}} \right)}}{{10}} = \frac{{200\sqrt 3 }}{3}\,{\text{m/s}} \cr & = \frac{{200\sqrt 3 }}{3} \times \frac{{18}}{5}\,{\text{km/hr}} \cr & = {\text{24}}\sqrt 3 \,{\text{km/hr}} \cr} $$.

46. The angle of elevation of the sun, when the length of the shadow of a tree √3 times the height of the tree, is:
a) 30º
b) 45º
c) 60º
d) 90º

View Answer  Discussion

Answer: a
Explanation:

Let ∠ACB = θ
$$\frac{{AC}}{{AB}} = \cot \theta $$
$$\frac{{AC}}{{AB}} = \sqrt 3 $$
$$\cot {30^ \circ } = \sqrt 3 $$
θ = 30°

47. The angle of elevation of the top of a tower from a certain point is 30°. If the observed moves 20 m towards the tower, the angle of elevation the angle of elevation of top of the tower increases by 15°. The height of the tower is
a) 17.3 m
b) 21.9 m
c) 27.3 m
d) 30 m

View Answer  Discussion

Answer: c
Explanation:

Let AB be the tower and C and D be the points of observation.
Then, ∠ACB = 30°, ∠ADB = 45° and CD = 20m
Let AB = h then,
$$\eqalign{ & \frac{{AB}}{{AC}} = \tan 30^\circ = \frac{1}{{\sqrt 3 }} \cr & \Rightarrow AC = AB \times \sqrt 3 = h\sqrt 3 {\kern 1pt} {\text{And,}} \cr & \Rightarrow \frac{{AB}}{{AD}} = \tan 45^\circ = 1 \cr & \Rightarrow AD = AB = h \cr & \, \, \, \, \, CD = 20 \cr & \Rightarrow \left( {AC - AD} \right) = 20 \cr & \Rightarrow h\sqrt 3 - h = 20 \cr & h = \frac{{20}}{{\left( {\sqrt 3 - 1} \right)}} \times \frac{{\left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 + 1} \right)}} \cr & = 10\left( {\sqrt 3 + 1} \right){\text{m}} \cr & = \left( {10 \times 2.73} \right){\text{m}} \cr & = 27.3 {\text{m}} \cr} $$

48. On the same side of tower, two objects are located. Observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, the distance between the objects is-
a) 63.5 m
b) 76.9 m
c) 86.7 m
d) 90 m

View Answer  Discussion

Answer: a
Explanation:

Let AB be the tower and C and D be the objects.
Then, AB = 150 m, ∠ACB = 45° and ∠ADB = 60°
$$\eqalign{ & \frac{{AB}}{{AD}} = \tan {60^ \circ } = \sqrt 3 \cr & \Rightarrow AD = \frac{{AB}}{{\sqrt 3 }} = \frac{{150}}{{\sqrt 3 }} \cr & \frac{{AB}}{{AC}} = \tan {45^ \circ } = 1 \cr & \Rightarrow AC = AB = 150{\text{ m}} \cr & CD = \left( {AC - AD} \right) \cr & = \left( {150 - \frac{{150}}{{\sqrt 3 }}} \right){\text{m}} \cr & = \left[ {\frac{{150\left( {\sqrt 3 - 1} \right)}}{{\sqrt 3 }} \times \frac{{\sqrt 3 }}{{\sqrt 3 }}} \right]{\text{m}} \cr & = 50\left( {3 - \sqrt 3 } \right){\text{m}} \cr & = \left( {50 \times 1.27} \right){\text{m}} \cr & = 63.5\,{\text{m}} \cr} $$

49. The angle of depression of a point situated at a distance of 70m from the base of a tower is 60°. The height of the tower is-
a) \[35\sqrt 3 {\text{ m}}\]
b) \[70\sqrt 3 {\text{ m}}\]
c) \[\frac{{70\sqrt 3 }}{3}{\text{ m}}\]
d) \[{\text{70 m}}\]

View Answer  Discussion

Answer: b
Explanation:

Length of the tower AB = h meter.
$$\eqalign{ & \angle DAC = \angle ACB = {60^ \circ } \cr & BC = 70{\text{ meter}} \cr & {\text{In }}\vartriangle {\text{ABC,}} \cr & {\text{tan }}{60^ \circ } = \frac{{AB}}{{BC}} \cr & \sqrt 3 = \frac{h}{{70}} \cr & h = 70\sqrt 3 {\text{ meter}} \cr} $$

50. A man on the top of a vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower ?
a) 14 min. 35 sec.
b) 15 min. 49 sec.
c) 16 min. 23 sec.
d) 18 min. 5 sec.

View Answer  Discussion

Answer: c
Explanation:

Let AB be the tower and C and D be the two positions of the car.
Then, \[\angle ACB = {45^ \circ },\]    \[\angle ADB = {30^ \circ }\]
Let, AB = h, CD = x and AC = y
$$\eqalign{ & \frac{{AB}}{{AC}} = \tan {45^ \circ } = 1 \cr & \Rightarrow \frac{h}{y} = 1 \cr & \Rightarrow y = h \cr & \frac{{AB}}{{AD}} = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }} \cr & \frac{h}{{x + y}} = \frac{1}{{\sqrt 3 }} \cr & x + y = \sqrt 3 h \cr & x = \left( {x + y - y} \right) \cr & \,\,\,\,\,\,\, = \sqrt 3 h - h \cr & \,\,\,\,\,\,\, = h\left( {\sqrt 3 - 1} \right) \cr} $$
Now, $$h\left( {\sqrt 3 - 1} \right)$$   is covered in 12 min.
So, h will be covered in→
$$\eqalign{ & \left[ {\frac{{12}}{{h\left( {\sqrt 3 - 1} \right)}} \times h} \right] \cr & = \frac{{12}}{{\left( {\sqrt 3 - 1} \right)}}\min \cr & = \left( {\frac{{1200}}{{73}}} \right)\min \cr & = 16\min ,\,\,23\sec \cr} $$

51. A man on the top of a vertical observation tower observers a car moving at a uniform speed coming directly towards it. If it takes 8 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower?
a) 8 min 17 second
b) 10 min 57 second
c) 14 min 34 second
d) 12 min 23 second

View Answer  Discussion

Answer: b
Explanation:

Consider the diagram shown above. Let AB be the tower. Let D and C be the positions of the car.
Then, ∠ ADC = 30° , ∠ ACB = 45°
Let AB = h, BC = x, CD = y
$$\eqalign{ & \tan {45^ \circ } = \frac{{AB}}{{BC}} = \frac{h}{x} \cr & \Rightarrow 1 = \frac{h}{x} \cr & \Rightarrow h = x\,......\left( 1 \right) \cr & \tan {30^ \circ } = \frac{{AB}}{{BD}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{AB}}{{\left( {BC + CD} \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{h}{{x + y}} \cr & \Rightarrow \frac{1}{{\sqrt 3 }} = \frac{h}{{x + y}} \cr & x + y = \sqrt 3 \,h \cr & y = \sqrt 3 \,h - x \cr} $$
$$ y = \sqrt 3 \,h - h$$     ( Substituted the value of x from equation 1 )
$$ y = h\left( {\sqrt 3 - 1} \right)$$
Given that distance y is covered in 8 minutes.
i.e, distance $$h\left( {\sqrt 3 - 1} \right)$$   is covered in 8 minutes.
Time to travel distance x
= Time to travel distance h (∵ Since x = h as per equation 1).
Let distance h is covered in t minutes.
since distance is proportional to the time when the speed is constant, we have
$$\eqalign{ & h\left( {\sqrt 3 - 1} \right) \propto 8\,......\left( {\text{A}} \right) \cr & h \propto t\,..............\left( {\text{B}} \right) \cr & \frac{{\left( {\text{A}} \right)}}{{\left( {\text{B}} \right)}} \Rightarrow \frac{{h\left( {\sqrt 3 - 1} \right)}}{h} = \frac{8}{t} \cr & \Rightarrow \left( {\sqrt 3 - 1} \right) = \frac{8}{t} \cr & \Rightarrow t = \frac{8}{{\left( {\sqrt 3 - 1} \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\, = \frac{8}{{\left( {1.73 - 1} \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\, = \frac{8}{{.73}} \cr & \,\,\,\,\,\,\,\,\,\,\, = \frac{{800}}{{73}}\,{\text{minutes}} \cr & \,\,\,\,\,\,\,\,\,\,\, = 10\frac{{70}}{{73}}\,{\text{minutes}} \cr & \approx {\text{10}}\,{\text{minutes}}\,{\text{57}}\,{\text{seconds}} \cr} $$

52. Two vertical poles are 200 m apart and the height of one is double that of the other. From the middle point of the line joining their feet, an observer finds the angular elevations of their tops to be complementary. Find the heights of the poles.
a) 141 m and 282 m
b) 70.5 m and 141 m
c) 65 m and 130 m
d) 130 m and 260 m

View Answer  Discussion

Answer: b
Explanation:

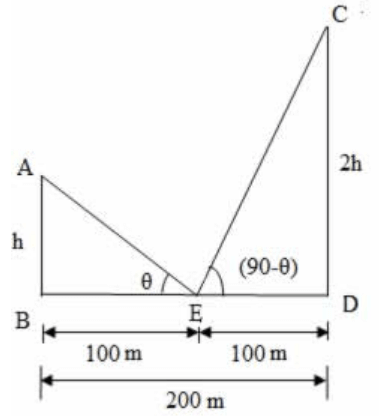
Let AB and CD be the poles with heights h and 2h respectively.
Given that distance between the poles, BD = 200 m
Let E be the middle point of BD,
∠ AEB = $$\theta $$
∠ CED = (90 - $$\theta $$)   ( given that angular elevations are complementary)
Since E is the middle point of BD, we have BE = ED = 100 m
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABE, \cr & \tan \theta = \frac{{AB}}{{BE}} \cr & \tan \theta = \frac{h}{{100}} \cr & h = 100\tan \theta \,......\left( 1 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta EDC, \cr & \tan\left( {90 - \theta } \right) = \frac{{CD}}{{ED}} \cr} $$
$$\cot \theta = \frac{{2h}}{{100}}$$     $$\left[ {\because \tan \left( {90 - \theta } \right) = \cot \theta } \right]$$
$$\eqalign{ & 2h = 100\cot \theta \,......\left( 2 \right) \cr & \left( 1 \right) \times \left( 2 \right) \cr} $$
$$ \Rightarrow 2{h^2} = {100^2}$$     $$\left[ {\because \tan \theta \times \cot\theta = \tan\theta \times \frac{1}{{\tan \theta }} = 1} \right]$$
$$\eqalign{ & \Rightarrow \sqrt 2 \,h = 100 \cr & \Rightarrow h = \frac{{100}}{{\sqrt 2 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{100 \times \sqrt 2 }}{{\sqrt 2 \times \sqrt 2 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 50\sqrt 2 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 50 \times 1.41 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 70.5 \cr & \Rightarrow 2h = 2 \times 70.5 = 141 \cr} $$
i.e. the height of the poles are 70.5 m and 141 m.

53. From the foot and the top of a building of height 230 m, a person observes the top of a tower with angles of elevation of b and a respectively. What is the distance between the top of these buildings if tan a = $$\frac{5}{{12}}$$ and tan b = $$\frac{4}{{5}}$$
a) 400 m
b) 250 m
c) 600 m
d) 650 m

View Answer  Discussion

Answer: d
Explanation:

Let ED be the building and AC be the tower.
Given that ED = 230 m, ∠ADC = b, ∠AEB = a
Also given that tan a = $$\frac{5}{{12}}$$ and tan b = $$\frac{4}{{5}}$$
Let AC = h
Required Distance = Distance between the top of these buildings = AE
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABE, \cr & \tan \left( a \right) = \frac{{AB}}{{BE}} \cr} $$
$$ \Rightarrow \frac{5}{{12}} = \frac{{\left( {h - 230} \right)}}{{BE}}$$     [ tan(a) = $$\frac{5}{{12}}$$ (given), AB = (AC - BC) = (AC - ED) = (h - 230)]
$$\eqalign{ & \Rightarrow BE = \frac{{12\left( {h - 230} \right)}}{5}\,.....\left( 1 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ACD, \cr & \tan \left( b \right) = \frac{{AC}}{{CD}} \cr} $$
$$ \Rightarrow \frac{4}{5} = \frac{h}{{CD}}$$    [ tan(b) = $$\frac{4}{5}$$ (given), AC = h]
$$\eqalign{ & \Rightarrow CD = \frac{{5h}}{4}\,.....\left( 2 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{diagram,}}\,BE = CD \cr} $$
$$ \Rightarrow \frac{{12\left( {h - 230} \right)}}{5} = \frac{{5h}}{4}$$     (from equation 1 & 2)
$$\eqalign{ & \Rightarrow 48h - \left( {4 \times 12 \times 230} \right) = 25h \cr & \Rightarrow 23h = \left( {4 \times 12 \times 230} \right) \cr & \Rightarrow h = \frac{{\left( {4 \times 12 \times 230} \right)}}{{23}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 480\,{\text{m}}\,......\left( 3 \right) \cr & AB = \left( {AC - BC} \right) \cr} $$
$$\,\,\,\,\,\,\,\,\,\,\,\, = \left( {480 - 230} \right)$$    [ Since AC = h = 480 (from 3) and BC = ED = 230 m(given)]
$$\,\,\,\,\,\,\,\,\,\,\,\, = 250\,{\text{m}}$$
In the triangle ABE, tan(a) =$$\frac{5}{{12}}$$ . Let's figure out the value of sin(a) now.
Consider a triangle with opposite side = 5 and adjacent side = 12 such that tan(a) = $$\frac{5}{{12}}$$
$$\eqalign{ & {\text{hypotenuse}} = \sqrt {{5^2} + {{12}^2}} = 13 \cr & {\text{i}}{\text{.e}}{\text{.,}} \cr & \sin \left( a \right) = \frac{{{\text{opposite}}\,{\text{side}}}}{{{\text{hypotenuse}}}} = \frac{5}{{13}} \cr} $$
We have seen that $$\sin \left( a \right) = \frac{5}{{13}}$$
$$\eqalign{ & \frac{{AB}}{{AE}} = \frac{5}{{13}} \cr & AE = AB \times \frac{{13}}{5} \cr & = 250 \times \frac{{13}}{5} \cr & = 650\,{\text{m}} \cr} $$
i.e., Distance between the top of the buildings = 650 m

54. From a tower of 80 m high, the angle of depression of a bus is 30°. How far is the bus from the tower?
a) 40 m
b) 138.4 m
c) 46.24 m
d) 160 m

View Answer  Discussion

Answer: b
Explanation:

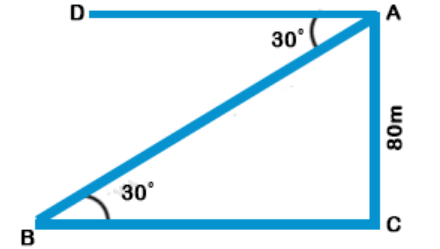
Let AC be the tower and B be the position of the bus.
Then BC = the distance of the bus from the foot of the tower.
Given that height of the tower, AC = 80 m and the angle of depression, ∠DAB = 30°
∠ABC = ∠DAB = 30° (because DA || BC)
$$\eqalign{ & \tan {30^ \circ } = \frac{{AC}}{{BC}} \cr & \tan {30^ \circ } = \frac{{80}}{{BC}} \cr & BC = \frac{{80}}{{\tan {{30}^ \circ }}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{80}}{{\left( {\frac{1}{{\sqrt 3 }}} \right)}} \cr & = 80 \times 1.73 = 138.4\,{\text{m}} \cr} $$
i.e., Distance of the bus from the foot of the tower = 138.4 m

55. The elevation of the summit of a mountain from its foot is 45°. After ascending 2 km towards the mountain upon an incline of 30°,the elevation changes to 60°. What is the approximate height of the mountain?
a) 1.2 km
b) 0.6 km
c) 1.4 km
d) 2.7 km

View Answer  Discussion

Answer: d
Explanation:

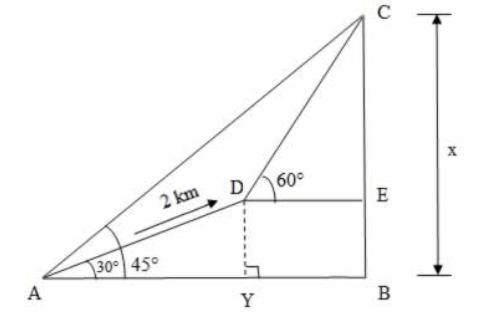
Let A be the foot and C be the summit of a mountain.
Given that ∠CAB = 45°
From the diagram, CB is the height of the mountain. Let CB = x
Let D be the point after ascending 2 km towards the mountain such that AD = 2 km and given that ∠DAY = 30°
It is also given that from the point D, the elevation is 60°
i.e., ∠CDE = 60°
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABC, \cr & \tan {45^ \circ } = \frac{{CB}}{{AB}} \cr} $$
$$ \Rightarrow 1 = \frac{x}{{AB}}$$    [ CB = x(the height of the mountain)]
$$\eqalign{ & \Rightarrow AB = x\,......\left( 1 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta AYD, \cr & \sin {30^ \circ } = \frac{{DY}}{{AD}} \cr} $$
$$ \Rightarrow \frac{1}{2} = \frac{{DY}}{2}$$    ( Given that AD = 2)
$$\eqalign{ & \Rightarrow DY = 1\,.......\left( 2 \right) \cr & \cos {30^ \circ } = \frac{{AY}}{{AD}} \cr} $$
$$ \Rightarrow \frac{{\sqrt 3 }}{2} = \frac{{AY}}{2}$$    ( Given that AD = 2)
$$\eqalign{ & \Rightarrow AY = \sqrt 3 \,......\left( 3 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta CED, \cr & \tan {60^ \circ } = \frac{{CE}}{{DE}} \cr} $$
$$ \Rightarrow \tan {60^ \circ } = \frac{{\left( {CB - EB} \right)}}{{YB}}$$     [ CE = (CB - EB) and DE = YB)]
$$ \Rightarrow \tan {60^ \circ } = \frac{{\left( {CB - DY} \right)}}{{AB - AY}}$$     [ EB = DY and YB = (AB - AY)]
$$ \Rightarrow \tan {60^ \circ } = \frac{{\left( {x - 1} \right)}}{{\left( {x - \sqrt 3 } \right)}}$$
[ CB = x, DY = 1(eq:2), AB = x(eq:1) and AY = $${\sqrt 3 }$$ (eq:3)]
$$\eqalign{ & \sqrt 3 = \frac{{\left( {x - 1} \right)}}{{\left( {x - \sqrt 3 } \right)}} \cr & x\sqrt 3 - 3 = x - 1 \cr & x\left( {\sqrt 3 - 1} \right) = 2 \cr & 0.73x = 2 \cr & x = \frac{2}{{0.73}} = 2.7 \cr} $$

56. If the height of a vertical pole is $$\sqrt 3 $$ times the length of its shadow on the ground, then the angle of elevation of the sun at that time is
a) 30°
b) 60°
c) 45°
d) 75°

View Answer  Discussion

Answer: b
Explanation: Let AB be a vertical pole and let its shadow be BC

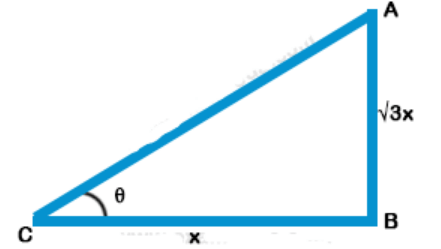
Let BC = x m, then length of pole = $$\sqrt 3 $$ x,
$$\theta $$ be the angle of elevation
$$\eqalign{ & {\text{tan}}\theta = \frac{{AB}}{{BC}} = \frac{{\sqrt 3 \,x}}{x} = \sqrt 3 \cr & = \tan {60^ \circ } \cr & \theta = {60^ \circ } \cr} $$

57. Two persons are 'a' meters apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
a) $$\frac{a}{4}$$
b) $$\frac{a}{{\sqrt 2 }}$$
c) $$a\sqrt 2 $$
d) $$\frac{a}{{2\sqrt 2 }}$$

View Answer  Discussion

Answer: d
Explanation: Let AB and CD are two persons standing ‘a’ meters apart P is the mid-point of BD and from M, the angles of elevation of A and C are complementary

$$\eqalign{ & {\text{In}}\,\,\Delta {\text{APB,}} \cr & \tan \theta = \frac{{AB}}{{BP}} = \frac{h}{{\frac{a}{2}}} = \frac{{2h}}{a} \cr & {\text{In}}\,\,\Delta {\text{CDP,}} \cr & \cot (90 - \theta ) = \frac{{PD}}{{CD}} = \frac{{\frac{a}{2}}}{{2h}} = \frac{a}{{4h}} \cr & {\text{We}}\,\,{\text{Know}}\,\,{\text{that,}} \cr & \tan \theta = \cot (90 - \theta ). \cr & \frac{{2h}}{a} = \frac{a}{{4h}} \cr & 8{h^2} = {a^2} \cr & h = \frac{a}{{2\sqrt 2 }} \cr} $$

58.If the angle of elevation of a tower from a distance of 100 metres from its foot is 60?, the height of the tower is
a) $$100\sqrt 3 \,m$$
b) $$\frac{{100}}{{\sqrt 3 }}\,m$$
c) $$50\sqrt 3 \,m$$
d) $$\frac{{200}}{{\sqrt 3 }}\,m$$

View Answer  Discussion

Answer: a
Explanation: Let AB be the tower and a point P at a distance of 100 m from its foot, angle of elevation of the top of the tower is 60°

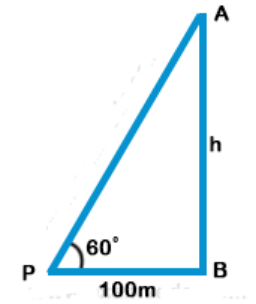
Let height of the tower = h
$$\eqalign{ & {\text{Then in right }}\Delta ABP \cr & \tan \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \frac{{AB}}{{PB}} \cr & \Rightarrow \tan {60^ \circ } = \frac{h}{{100}} \Rightarrow \sqrt 3 = \frac{h}{{100}} \cr & h = 100\sqrt 3 \cr & {\text{Height}}\,{\text{of}}\,{\text{tower}} = 100\sqrt 3 \cr} $$

59. The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart, the height of the light house is
a) $$\frac{{50}}{{\sqrt 3 + 1}}m$$
b) $$\frac{{50}}{{\sqrt 3 - 1}}m$$
c) $$50\left( {\sqrt 3 - 1} \right)m$$
d) $$50\left( {\sqrt 3 + 1} \right)m$$

View Answer  Discussion

60. The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
a) 25 $$\sqrt 3 $$
b) 50 $$\sqrt 3 $$
c) 75 $$\sqrt 3 $$
d) 150

View Answer  Discussion

61. If a 30 m ladder is placed against a 15 m wall such that it just reaches the top of the wall, then the elevation of the wall is equal to-
a) 45°
b) 30°
c) 60°
d) 50°

View Answer  Discussion

Answer: b
Explanation:

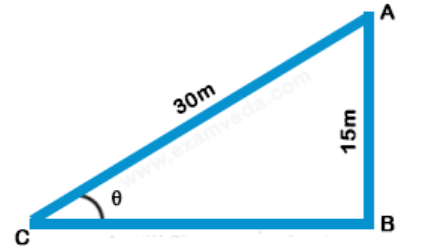
$$\eqalign{ & {\text{AC = 30 meter}} \cr & {\text{AB = 15 meter}} \cr & \angle {\text{ACB}} = \theta \cr & \sin \theta = \frac{{AB}}{{AC}} = \frac{{15}}{{30}} = \frac{1}{2} \cr & \sin \theta = \sin {30^ \circ } \cr & \theta = {30^ \circ } \cr} $$

62. The angles of elevation of the top of from two points P and Q at distance $${{m^2}}$$ and $${{n^2}}$$ respectively, from the base and in the same straight line with it are complementary. The height of the tower is-
a) $${\left( {mn} \right)^{\frac{1}{2}}}$$
b) $$m{n^{\frac{1}{2}}}$$
c) $${m^{\frac{1}{2}}}n$$
d) $$mn$$

View Answer  Discussion

Answer: d
Explanation:

$$\eqalign{ & {\text{tan }}\theta = \frac{H}{{{m^2}}} \cr & \tan \left( {90^ \circ - \theta } \right) = \frac{H}{{{n^2}}} \cr & \cot \theta = \frac{H}{{{n^2}}} \cr & \tan \theta .\cot \theta = \frac{H}{{{m^2}}} \times \frac{H}{{{n^2}}} \cr & \frac{H}{{{m^2}}} \times \frac{H}{{{n^2}}} = 1 \cr & {H^2} = {m^2}{n^2} \cr & H = mn \cr} $$

63. A boy is standing at the top of the tower and another boy is at the ground at some distance from the foot of the tower, then the angle of elevation and depression between the boys when both look at a each other will be-
a) Equal
b) Angle of elevation will be greater
c) Cannot be predicted for relation
d) Angle of depression will be greater

View Answer  Discussion

Answer: a
Explanation:

$$\eqalign{ & {\text{Here, AD is parallel to BC and AC is a transversal}}{\text{.}} \cr & {\theta _1} = {\theta _2} \cr} $$

64.The angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. The height of the cloud is-
a) 200 m
b) 300 m
c) 400 m
d) 600 m

View Answer  Discussion

Answer: a
Explanation:

$$\eqalign{ & {\text{Let, }}AC = H{\text{ }}m \cr & OA = {\text{ }}a{\text{ }}m \cr & \tan {\text{ }}{30^ \circ } = \frac{1}{{\sqrt 3 }} = \frac{H}{a} \cr} $$
$$\tan {60^ \circ } = \sqrt 3 $$    $$ = \frac{{H + 200 + 200}}{a}$$
$$\eqalign{ & \frac{{H + 400}}{{\sqrt 3 H}} = \sqrt 3 \cr & H + 400 = 3H \cr & 2H = 400\,m \cr & H = 200\,m \cr} $$
Height of cloud above lake = 200 m

65. A man is watching from the top of tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man’s eye when at a distance of 60 meters from the tower. After 5 seconds, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming that it is running in still water?
a) 32 kmph
b) 36 kmph
c) 38 kmph
d) 40 kmph

View Answer  Discussion

Answer: a
Explanation:

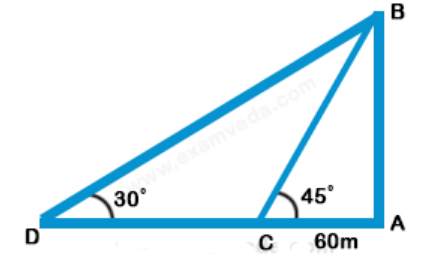
Let AB be the tower and C and D be the two positions of the boats.
Then, $$\angle {\text{ACB = }}{45^ \circ },$$    $$\angle ADB = {30^ \circ }$$     and AC = 60 m
Let, AB = h
$$\eqalign{ & {\text{Then,}}\frac{{AB}}{{AC}} = \tan {45^ \circ } = 1 \cr & \Rightarrow AB = AC \cr & \Rightarrow h = 60\,m \cr & {\text{And}}\frac{{AB}}{{AD}} = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }} \cr & AD = \left( {AB \times \sqrt 3 } \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 60\sqrt 3 \,m \cr & CD = \left( {AD - AC} \right) \cr & \,\,\,\,\,\,\,\,\,\,\, = 60\left( {\sqrt 3 - 1} \right)\,m \cr & {\text{Hence, required speed }} \cr & {\text{ = }}\left[ {\frac{{60\left( {\sqrt 3 - 1} \right)}}{5}} \right]{\text{m/s}} \cr & {\text{ = }}\left( {12 \times 0.73} \right){\text{m/s}} \cr & = \left( {12 \times 0.73 \times \frac{{18}}{5}} \right){\text{km/hr}} \cr & = {\text{31}}{\text{.5km/hr }} \approx {\text{ 32km/hr}} \cr} $$

66. The length of shadow of a tower on the plane ground is $$\sqrt 3 $$ times the height of the tower. The angle of elevation of sun is
a) 45°
b) 30°
c) 60°
d) 90°

View Answer  Discussion

Answer: b
Explanation: Let AB be tower and BC be its shadow
Let AB = x

$$\eqalign{ & {\text{Then}}\,BC = \sqrt 3 \times x = \sqrt 3 \,x \cr & \tan \theta = \frac{{AB}}{{BC}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{x}{{\sqrt 3 \,x}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \tan {30^ \circ } \cr & \theta = {30^ \circ } \cr} $$
Angle of elevation of the sun$${\text{ = }}{30^ \circ }$$

67. The length of the shadow of a tower standing on level ground is found to 2x meter longer when the sun’s elevation is 30° than when it was 45 °. The height of the tower in meters is
a) $$\left( {\sqrt 3 + 1} \right)\,x$$
b) $$\left( {\sqrt 3 - 1} \right)\,x$$
c) $$2\sqrt 3 \,x$$
d) $$3\sqrt 2 \,x$$

View Answer  Discussion

Answer: a
Explanation: AB is a tower
BD and BC are its shadows and CD = 2x

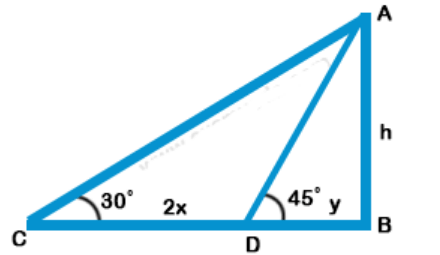
$$\eqalign{ & \tan {45^ \circ } = \frac{{AB}}{{DB}} \cr & \Rightarrow 1 = \frac{h}{y} \Rightarrow y = h \cr & {\text{and}}\tan {30^ \circ } = \frac{{AB}}{{CB}} \cr & \frac{1}{{\sqrt 3 }} = \frac{h}{{2x + y}} \cr & 2x + y = \sqrt 3 \,h \cr & \sqrt 3 \,h - h = 2x \cr & h\left( {\sqrt 3 - 1} \right) = 2x \cr & \Rightarrow h = \frac{{2x}}{{\sqrt 3 - 1}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{2x\left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{2x\left( {\sqrt 3 + 1} \right)}}{{3 - 1}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{2x\left( {\sqrt 3 + 1} \right)}}{2} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = x\left( {\sqrt 3 + 1} \right) \cr} $$

68. If the angle of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with It are complementary, then the height of the tower is
a) $$ab$$
b) $$\sqrt {ab} $$
c) $$\frac{a}{b}$$
d) $$\sqrt {\frac{a}{b}} $$

View Answer  Discussion

Answer: b
Explanation: Let AB be the tower and P and Q are two points such that PB = a and QB = b and angles of elevation are $$\theta $$ and (90° – $$\theta $$)
Let height of tower = h

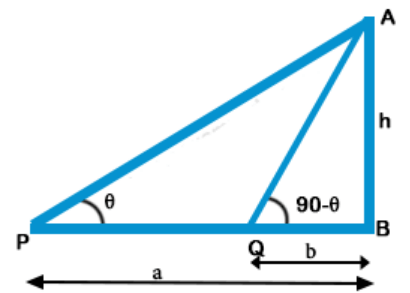
$$\eqalign{ & {\text{Then}}\,{\text{in}}\,{\text{right}}\,\Delta APB, \cr & \tan \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \frac{{AB}}{{PB}} \cr & = \frac{h}{a}\,............\left( {\text{i}} \right) \cr & {\text{Similarly in right }}\Delta AQB, \cr & \tan \left( {{{90}^ \circ } - \theta } \right) = \frac{{AB}}{{QB}} = \frac{h}{b} \cr & \Rightarrow \cot \theta = \frac{h}{b}\,...........\left( {{\text{ii}}} \right) \cr & {\text{Multiplying }}\left( {\text{i}} \right){\text{ and }}\left( {{\text{ii}}} \right) \cr & \tan \theta \cot \theta = \frac{h}{a} \times \frac{h}{b} \cr & 1 = \frac{{{h^2}}}{{ab}} \cr & {h^2} = ab \cr & h = \sqrt {ab} \cr & {\text{Height}}\,{\text{of}}\,{\text{tower}} = \sqrt {ab} \cr} $$

69. The angle of elevation of the top of a lighthouse 60 m high, from two points on the ground on its opposite sides are 45° and 60°. What is the distance between these two points?
a) 45 m
b) 30 m
c) 103.8 m
d) 94.6 m

View Answer  Discussion

Answer: d
Explanation:

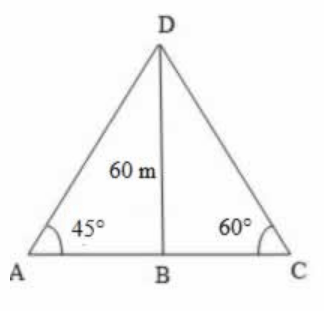
Let BD be the lighthouse and A and C be the two points on ground.
Then, BD, the height of the lighthouse = 60 m
∠BAD = 45°, ∠BCD = 60°
$$\eqalign{ & \tan {45^ \circ } = \frac{{BD}}{{BA}} \cr & 1 = \frac{{60}}{{BA}} \cr & BA = 60\,m\,........\left( {\text{i}} \right) \cr & \tan {60^ \circ } = \frac{{BD}}{{BC}} \cr & \sqrt 3 = \frac{{60}}{{BC}} \cr & \Rightarrow BC = \frac{{60}}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{60 \times \sqrt 3 }}{{\sqrt 3 \times \sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{60\sqrt 3 }}{3} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 20\sqrt 3 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 20 \times 1.73 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 34.6\,m\,..........\left( {{\text{ii}}} \right) \cr} $$
Distance between the two points A and C
= AC = BA + BC
= 60 + 34.6 [ Substituted value of BA and BC from (i) and (ii)]
= 94.6 m

70. On the same side of a tower, two objects are located. Observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 600 m, the distance between the objects is approximately equal to :
a) 272 m
b) 284 m
c) 288 m
d) 254 m

View Answer  Discussion

Answer: d
Explanation:

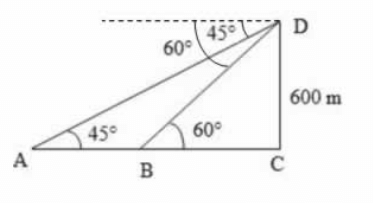
Let DC be the tower and A and B be the objects as shown above.
Given that DC = 600 m, ∠DAC = 45°, ∠DBC = 60°
$$\eqalign{ & \tan {60^ \circ } = \frac{{DC}}{{BC}} \cr & \sqrt 3 = \frac{{600}}{{BC}} \cr & BC = \frac{{600}}{{\sqrt 3 }}\,..........\,\left( {\text{i}} \right) \cr & \tan {45^ \circ } = \frac{{DC}}{{AC}} \cr & 1 = \frac{{600}}{{AC}} \cr & AC = 600\,............\,\left( {{\text{ii}}} \right) \cr} $$
Distance between the objects
$$ = AC = \left( {AC - BC} \right)$$
$$ = 600 - \frac{{600}}{{\sqrt 3 }}$$   [ from (1) and (ii)]
$$\eqalign{ & = 600\left( {1 - \frac{1}{{\sqrt 3 }}} \right) \cr & = 600\left( {\frac{{\sqrt 3 - 1}}{{\sqrt 3 }}} \right) \cr & = 600\left( {\frac{{\sqrt 3 - 1}}{{\sqrt 3 }}} \right) \times \frac{{\sqrt 3 }}{{\sqrt 3 }} \cr & = \frac{{600\sqrt 3 \left( {\sqrt 3 - 1} \right)}}{3} \cr & = 200\sqrt 3 \left( {\sqrt 3 - 1} \right) \cr & = 200\left( {3 - \sqrt 3 } \right) \cr & = 200\left( {3 - 1.73} \right) \cr & = 254\,m \cr} $$

71. The angle of depression of a car parked on the road from the top of a 150 m high tower is 30°. The distance of the car from the tower (in metres) is
a) 50 $$\sqrt 3 $$
b) 150 $$\sqrt 3 $$
c) 100 $$\sqrt 3 $$
d) 75

View Answer  Discussion

72. If the altitude of the sun is at 60°, then the height of the vertical tower that will cast a shadow of length 30 m is
a) $$30\sqrt 3 \,m$$
b) $$15\,m$$
c) $$\frac{{30}}{{\sqrt 3 }}\,m$$
d) $$15\sqrt 2 \,m$$

View Answer  Discussion

Answer: a
Explanation: Let AB be tower and a point P distance of 30 m from its foot of the tower which form an angle of elevation pf the sun of 60°

$$\eqalign{ & {\text{Let height of tower }}AB = h \cr & {\text{Then in right }}\Delta APB, \cr & \tan \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \frac{{AB}}{{PB}} \cr & \Rightarrow \tan {60^ \circ } = \frac{h}{{30}} \cr & \sqrt 3 = \frac{h}{{30}} \cr & h = 30\sqrt 3 \cr} $$
Height of the tower $$ = 30\sqrt 3 \,m$$

73. The tops of two poles of height 16 m and 10 m are connected by a wire of length l metres. If the wire makes an angle of 30° with the horizontal, then l =
a) 26
b) 16
c) 12
d) 10

View Answer  Discussion

Answer: c
Explanation: Let AB and CD are two poles AB = 10 m and CD = 16 m

AC is wire which makes an angle of 30° with the horizontal
Let BD = x, then AE = x
CE = CD - ED = CD - AB = 16 - 10 = 6m
$$\eqalign{ & {\text{Now}}\,{\text{in}}\,\Delta ACE \cr & \sin {30^ \circ } = \frac{{CE}}{{AC}} = \frac{6}{l} \cr & \frac{1}{2} = \frac{6}{l} \cr & l = 2 \times 6 = 12\,m \cr} $$

74. The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes x metres less. The value of x is
a) $$100\,m$$
b) $$100\sqrt 3 \,m$$
c) $$100\left( {\sqrt 3 - 1} \right)\,m$$
d) $$\frac{{100}}{{\sqrt 3 }}\,m$$

View Answer  Discussion

Answer: c
Explanation: Let AB be tower and AB = 100 m and angles of elevation of A at C and D are 30° and 45° respectively and CD = x
Let BD = y

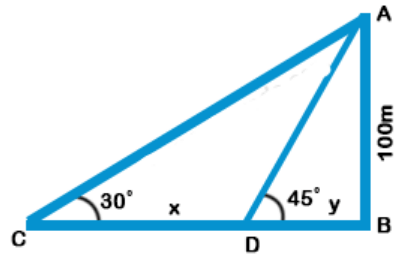
$$\eqalign{ & {\text{Now in right }}\Delta ADB, \cr & \tan \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \frac{{AB}}{{DB}} \cr & \tan {45^ \circ } = \frac{{100}}{y} \cr & \Rightarrow 1 = \frac{{100}}{y} \cr & \Rightarrow y = 100 \cr & {\text{Similarly in right }}\Delta ACB, \cr & \tan {30^ \circ } = \frac{{AB}}{{CB}} \cr & \frac{1}{{\sqrt 3 }} = \frac{{100}}{{y + x}} \cr & \frac{1}{{\sqrt 3 }} = \frac{{100}}{{100 + x}} \cr & 100 + x = 100\sqrt 3 \cr & x = 100\sqrt 3 - 100 \cr & x = 100\left( {\sqrt 3 - 1} \right)\,m \cr} $$

75. The angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance 'd' towards the foot of the tower the angle of elevation is found to be β. The height of the tower is:
a) $$\frac{d}{{\cot \alpha + \cot \beta }}$$
b) $$\frac{d}{{\cot \alpha - \cot \beta }}$$
c) $$\frac{d}{{\tan \beta - \operatorname{tant} \alpha }}$$
d) $$\frac{d}{{\tan \beta + \operatorname{tant} \alpha }}$$

View Answer  Discussion

Answer: b
Explanation: Let AB be the tower and C is a point such that the angle of elevation of A is α.
After walking towards the foot B of the tower, at D the angle of elevation is β.
Let h be the height of the tower and DB = x Now in ΔACB,

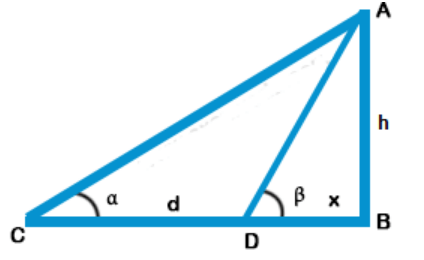
$$\eqalign{ & \tan \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \frac{{AB}}{{CB}} \cr & \tan \alpha = \frac{h}{{d + x}} \cr & \Rightarrow d + x = \frac{h}{{\tan \alpha }} \cr & \Rightarrow d + x = h\cot \alpha \cr & \Rightarrow x = h\cot \alpha - d\,.......\left( {\text{i}} \right) \cr & {\text{Similarly in right }}\Delta ADB, \cr & \tan \beta = \frac{h}{x} \cr & \Rightarrow x = \frac{h}{{\tan \beta }} \cr & \Rightarrow x = h\cot \beta \,.........({\text{ii}}) \cr & {\text{From}}\,\left( {\text{i}} \right)\,{\text{and}}\,\left( {{\text{ii}}} \right) \cr & h\cot \alpha - d = h\cot \beta \cr & h\cot \alpha - h\cot \beta = d \cr & h\left( {\cot \alpha - \cot \beta } \right) = d \cr & h = \frac{d}{{\cot \alpha - \cot \beta }} \cr} $$
Height of the tower $$ = \frac{d}{{\cot \alpha - \cot \beta }}$$

76. From a point P on a level ground, the angle of elevation of the top tower is 30º. If the tower is 200 m high, the distance of point P from the foot of the tower is:
a) 346 m
b) 400 m
c) 312 m
d) 298 m

View Answer  Discussion

Answer: a
Explanation:

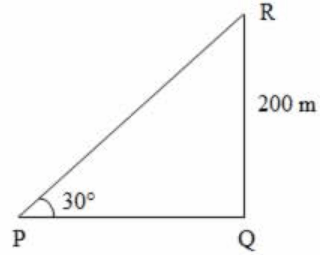
$$\eqalign{ & \tan {30^ \circ } = \frac{{RQ}}{{PQ}} \cr & \frac{1}{{\sqrt 3 }} = \frac{{200}}{{PQ}} \cr & PQ = 200\sqrt 3 \cr & \,\,\,\,\,\,\,\,\,\, = 200 \times 1.73 \cr & \,\,\,\,\,\,\,\,\,\, = 346\,{\text{m}} \cr} $$

77. The angles of depression and elevation of the top of a wall 11 m high from top and bottom of a tree are 60° and 30° respectively. What is the height of the tree?
a) 22 m
b) 44 m
c) 33 m
d) None of these

View Answer  Discussion

Answer: b
Explanation:

Let DC be the wall, AB be the tree.
Given that ∠DBC = 30°, ∠DAE = 60°, DC = 11 m
$$\eqalign{ & \tan {30^ \circ } = \frac{{DC}}{{BC}} \cr & \frac{1}{{\sqrt 3 }} = \frac{{11}}{{BC}} \cr & BC = 11\sqrt 3 \,m \cr & AE = BC = 11\sqrt 3 \,m\,.....\left( 1 \right) \cr & \tan {60^ \circ } = \frac{{ED}}{{AE}} \cr} $$
$$\sqrt 3 = \frac{{ED}}{{11\sqrt 3 }}$$   [ Substituted value of AE from (1)]
$$\eqalign{ & ED = 11\sqrt 3 \times \sqrt 3 \cr & \,\,\,\,\,\,\,\,\,\, = 11 \times 3 \cr & \,\,\,\,\,\,\,\,\,\, = 33 \cr & {\text{Height}}\,{\text{of}}\,{\text{the}}\,{\text{tree}} \cr & = AB = EC = \left( {ED + DC} \right) \cr & = 33 + 11 \cr & = 44\,{\text{m}} \cr} $$

78. The angle of elevation of the top of the tower from a point on the ground is $${\sin ^{ - 1}}\left({\frac{3}{5}} \right).$$   If the point of observation is 20 meters away from the foot of the tower, what is the height of the tower?
a) 9 m
b) 18 m
c) 15 m
d) 12 m

View Answer  Discussion

79. A ladder 10 m long just reaches the top of a wall and makes an angle of 60° with the wall.Find the distance of the foot of the ladder from the wall $$\left( {\sqrt 3 = 1.73} \right)$$
a) 4.32 m
b) 17.3 m
c) 5 m
d) 8.65 m

View Answer  Discussion

Answer: d
Explanation:

Let BA be the ladder and AC be the wall as shown above.
Then the distance of the foot of the ladder from the wall = BC
Given that BA = 10 m, ∠ BAC = 60°
$$\eqalign{ & \sin {60^ \circ } = \frac{{BC}}{{BA}} \cr & \frac{{\sqrt 3 }}{2} = \frac{{BC}}{{10}} \cr & BC = 10 \times \frac{{\sqrt 3 }}{2} \cr & \,\,\,\,\,\,\,\,\,\, = 5 \times 1.73 \cr & \,\,\,\,\,\,\,\,\,\, = 8.65\,{\text{m}} \cr} $$

80. A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30º with the man's eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 45º. What is the distance between the base of the tower and the point P?
a) 9 units
b) $$3\sqrt 3 $$ units
c) Data inadequate
d) 12 units

View Answer  Discussion

Answer: c
Explanation:

$$\eqalign{ & \tan {45^ \circ } = \frac{{SR}}{{QR}} \cr & \tan {30^ \circ } = \frac{{SR}}{{PR}} = \frac{{SR}}{{\left( {PQ + QR} \right)}} \cr} $$
Two equations and 3 variables. Hence we can not find the required value with the given data.
(Note that if one of SR, PQ, QR is known, this becomes two equations and two variables and if that was the case, we could have found out the required value.)